Exploration and Exploitation in Organizational Learning

Abstract

This paper considers the relation between the exploration of new possibilities and the exploitation of old certainties in organizational learning. It examines some complications in allocating resources between the two, particularly those introduced by the distribution of costs and benefits across time and space, and the effects of ecological interaction. Two general situations involving the development and use of knowledge in organizations are modeled. The first is the case of mutual learning between members of an organization and an organizational code. The second is the case of learning and competitive advantage in competition for primacy. The paper develops an argument that adaptive processes, by refining exploitation more rapidly than exploration, are likely to become effective in the short run but self-destructive in the long run. The possibility that certain common organizational practices ameliorate that tendency is assessed.

Introduction

A central concern of studies of adaptive processes is the relation between the exploration of new possibilities and the exploitation of old certainties (Schumpeter 1934; Holland 1975; Kuran 1988). Exploration includes things captured by terms such as search, variation, risk taking, experimentation, play, flexibility, discovery, innovation. Exploitation includes such things as refinement, choice, production, efficiency, selection, implementation, execution. Adaptive systems that engage in exploration to the exclusion of exploitation are likely to find that they suffer the costs of experimentation without gaining many of its benefits. They exhibit too many undeveloped new ideas and too little distinctive competence. Conversely, systems that engage in exploitation to the exclusion of exploration are likely to find themselves trapped in suboptimal stable equilibria. As a result, maintaining an appropriate balance between exploration and exploitation is a primary factor in system survival and prosperity.

This paper considers some aspects of such problems in the context of organizations. Both exploration and exploitation are essential for organizations, but they compete for scarce resources. As a result, organizations make explicit and implicit choices between the two. The explicit choices are found in calculated decisions about alternative investments and competitive strategies. The implicit choices are buried in many features of organizational forms and customs, for example, in organizational procedures for accumulating and reducing slack, in search rules and practices, in the ways in which targets are set and changed, and in incentive systems. Understanding the choices and improving the balance between exploration and exploitation are complicated by the fact that returns from the two options vary not only with respect to their expected values, but also with respect to their variability, their timing, and their distribution within and beyond the organization. Processes for allocating resources between them, therefore, embody intertemporal, interinstitutional, and interpersonal comparisons, as well as risk preferences. The difficulties involved in making such comparisons lead to complications in specifying appropriate trade-offs, and in achieving them.

The Exploration / Exploitation Trade-Off

Exploration and Exploitation in Theories of Organizational Action

In rational models of choice, the balance between exploration and exploitation is discussed classically in terms of a theory of rational search (Radner and Rothschild 1975; Hey 1982). It is assumed that there are several alternative investment opportunities, each characterized by a probability distribution over returns that is initially unknown. Information about the distribution is accumulated over time, but choices must be made between gaining new information about alternatives and thus improving future returns (which suggests allocating part of the investment to searching among uncertain alternatives), and using the information currently available to improve present returns (which suggests concentrating the investment on the apparently best alternative). The problem is complicated by the possibilities that new investment alternatives may appear, that probability distributions may not be stable, or that they may depend on the choices made by others.

In theories of limited rationality, discussions of the choice between exploration and exploitation emphasize the role of targets or aspiration levels in regulating allocations to search (Cyert and March 1963). The usual assumption is that search is inhibited if the most preferred alternative is above (but in the neighborhood of) the target. On the other hand, search is stimulated if the most preferred known alternative is below the target. Such ideas are found both in theories of satisficing (Simon 1955) and in prospect theory (Kahneman and Tversky 1979). They have led to attempts to specify conditions under which target-oriented search rules are optimal (Day 1967). Because of the role of targets, discussions of search in the limited rationality tradition emphasize the significance of the adaptive character of aspirations themselves (March 1988).

In studies of organizational learning, the problem of balancing exploration and exploitation is exhibited in distinctions made between refinement of an existing technology and invention of a new one (Winter 1971; Levinthal and March 1981). It is clear that exploration of new alternatives reduces the speed with which skills at existing ones are improved. It is also clear that improvements in competence at existing procedures make experimentation with others less attractive (Levitt and March 1988). Finding an appropriate balance is made particularly difficult by the fact that the same issues occur at levels of a nested system—at the individual level, the organizational level, and the social system level.

In evolutionary models of organizational forms and technologies, discussions of the choice between exploration and exploitation are framed in terms of balancing the twin processes of variation and selection (Ashby 1960; Hannan and Freeman 1987). Effective selection among forms, routines, or practices is essential to survival, but so also is the generation of new alternative practices, particularly in a changing environment. Because of the links among environmental turbulence, organizational diversity, and competitive advantage, the evolutionary dominance of an organizational practice is sensitive to the relation between the rate of exploratory variation reflected by the practice and the rate of change in the environment. In this spirit, for example, it has been argued that the persistence of garbage-can decision processes in organizations is related to the diversity advantage they provide in a world of relatively unstable environments, when paired with the selective efficiency of conventional rationality (Cohen 1986).

The Vulnerability of Exploration

Compared to returns from exploitation, returns from exploration are systematically less certain, more remote in time, and organizationally more distant from the locus of action and adaption. What is good in the long run is not always good in the short run. What is good at a particular historical moment is not always good at another time. What is good for one part of an organization is not always good for another part. What is good for an organization is not always good for a larger social system of which it is a part. As organizations learn from experience how to divide resources between exploitation and exploration, this distribution of consequences across time and space affects the lessons learned. The certainty, speed, proximity, and clarity of feedback ties exploitation to its consequences more quickly and more precisely than is the case with exploration. The story is told in many forms. Basic research has less certain outcomes, longer time horizons, and more diffuse effects than does product development. The search for new ideas, markets, or relations has less certain outcomes, longer time horizons, and more diffuse effects than does further development of existing ones.

Because of these differences, adaptive processes characteristically improve exploitation more rapidly than exploration. These advantages for exploitation cumulate. Each increase in competence at an activity increases the likelihood of rewards for engaging in that activity, thereby further increasing the competence and the likelihood (Argyris and Schén 1978; David 1985). The effects extend, through network externalities, to others with whom the learning organization interacts (Katz and Shapiro 1986; David and Bunn 1988). Reason inhibits foolishness; learning and imitation inhibit experimentation. This is not an accident but is a consequence of the temporal and spatial proximity of the effects of exploitation, as well as their precision and interconnectedness.

Since performance is a joint function of potential return from an activity and present competence of an organization at it, organizations exhibit increasing returns to experience (Arthur 1984). Positive local feedback produces strong path dependence (David 1990) and can lead to suboptimal equilibria. It is quite possible for competence in an inferior activity to become great enough to exclude superior activities with which an organization has little experience (Herriott, Levinthal, and March 1985). Since long-run intelligence depends on sustaining a reasonable level of exploration, these tendencies to increase exploitation and reduce exploration make adaptive processes potentially self-destructive.

The Social Context of Organizational Learning

The trade-off between exploration and exploitation exhibits some special features in the social context of organizations. The next two sections of the present paper describe two simple models of adaptation, use them to elaborate the relation between exploitation and exploration, and explore some implications of the relation for the accumulation and utilization of knowledge in organizations. The models identify some reasons why organizations may want to control learning and suggest some procedures by which they do so.

Two distinctive features of the social context are considered. The first is the mutual learning of an organization and the individuals in it. Organizations store knowledge in their procedures, norms, rules, and forms. They accumulate such knowledge over time, learning from their members. At the same time, individuals in an organization are socialized to organizational beliefs. Such mutual learning has implications for understanding and managing the trade-off between exploration and exploitation in organizations. The second feature of organizational learning considered here is the context of competition for primacy. Organizations often compete with each other under conditions in which relative position matters. The mixed contribution of knowledge to competitive advantage in cases involving competition for primacy creates difficulties for defining and arranging an appropriate balance between exploration and exploitation in an organizational setting.

Mutual Learning in the Development of Knowledge

Organizational knowledge and faiths are diffused to individuals through various forms of instruction, indoctrination, and exemplification. An organization socializes recruits to the languages, beliefs, and practices that comprise the organizational code (Whyte 1957; Van Maanen 1973). Simultaneously, the organizational code is adapting to individual beliefs. This form of mutual learning has consequences both for the individuals involved and for an organization as a whole. In particular, the trade-off between exploration and exploitation in mutual learning involves conflicts between short-run and long-run concerns and between gains to individual knowledge and gains to collective knowledge.

A Model of Mutual Learning

Consider a simple model of the development and diffusion of organizational knowledge. There are four key features to the model:

1. There is an external reality that is independent of beliefs about it. Reality is described as having m dimensions, each of which has a value of 1 or —1. The (independent) probability that any one dimension will have a value of 1 is 0.5.
2. At each time period, beliefs about reality are held by each of n individuals in an organization and by an organizational code of received truth. For each of the m dimensions of reality, each belief has a value of 1, 0, or —1. This value may change over time.
3. Individuals modify their beliefs continuously as a consequence of socialization into the organization and education into its code of beliefs. Specifically, if the code is 0 on a particular dimension, individual belief is not affected. In each period in which the code differs on any particular dimension from the belief of an individual, individual belief changes to that of the code with probability, $p_1$. Thus, $p_1$, is a parameter reflecting the effectiveness of socialization, i.e., learning from the code. Changes on the several dimensions are assumed to be independent of each other.
4. At the same time, the organizational code adapts to the beliefs of those individuals whose beliefs correspond with reality on more dimensions than does the code. The probability that the beliefs of the code will be adjusted to conform to the dominant belief within the superior group on any particular dimension depends on the level of agreement among individuals in the superior group and on $p_2$. More precisely, if the code is the same as the majority view among those individuals whose overall knowledge score is superior to that of the code, the code remains unchanged. If the code differs from the majority view on a particular dimension at the start of a time period, the probability that it will be unchanged at the end of period is $(1 — p_2)^k$, where k (k > 0) is the number of individuals (within the superior group) who differ from the code on this dimension minus the number who do not. This formulation makes the effective rate of code learning dependent on k, which probably depends on n. In the present simulations, n is not varied. Thus, $p_2$ is a parameter reflecting the effectiveness of learning by the code. Changes on the several dimensions are assumed to be independent of each other.

Within this system, initial conditions include: a reality m-tuple (m dimensions, each of which has a value of 1 or —1, with independent equal probability); an organizational code m-tuple (m dimensions, each of which is initially 0); and n individual m-tuples (m dimensions, with values equal 1, 0, or —1, with equal probabilities).

Thus, the process begins with an organizational code characterized by neutral beliefs on all dimensions and a set of individuals with varying beliefs that exhibit, on average, no knowledge. Over time, the organizational code affects the beliefs of individuals, even while it is being affected by those beliefs. The beliefs of individuals do not affect the beliefs of other individuals directly but only through affecting the code. The effects of reality are also indirect. Neither the individuals nor the organizations experience reality. Improvement in knowledge comes by the code mimicking the beliefs (including the false beliefs) of superior individuals and by individuals mimicking the code (including its false beliefs).

Basic Properties of the Model in a Closed System

Consider such a model of mutual learning first within a closed system having fixed organizational membership and a stable reality. Since realizations of the process are subject to stochastic variability, repeated simulations using the same initial conditions and parameters are used to estimate the distribution of outcomes. In all of the results reported here, the number of dimensions of reality (m) is set at 30, the number of individuals (n) is set at 50, and the number of repeated simulations is 80. The quantitative levels of the results and the magnitude of the stochastic fluctuations reported depend on these specifications, but the qualitative results are insensitive to values of m and n.

Since reality is specified, the state of knowledge at any particular time period can be assessed in two ways. First, the proportion of reality that is correctly represented in the organizational code can be calculated for any period. This is the knowledge level of the code for that period. Second, the proportion of reality that is correctly represented in individual beliefs (on average) can be calculated for any period. This is the average knowledge level of the individuals for that period.

Within this closed system, the model yields time paths of organizational and individual beliefs, thus knowledge levels, that depend stochastically on the initial conditions and the parameters affecting learning. The basic features of these histories can be summarized simply: Each of the adjustments in beliefs serves to eliminate differences between the individuals and the code. Consequently, the beliefs of individuals and the code converge over time. As individuals in the organization become more knowledgeable, they also become more homogeneous with respect to knowledge. An equilibrium is reached at which all individuals and the code share the same (not necessarily accurate) belief with respect to each dimension. The equilibrium is stable.

Effects of learning rates. Higher rates of learning lead, on average, to achieving equilibrium earlier. The equilibrium level of knowledge attained by an organization also depends interactively on the two learning parameters. Figure 1 shows the results when we assume that $p_1$, is the same for all individuals. Slower socialization (lower $p_1$) leads to greater knowledge at equilibrium than does faster socialization, particularly when the code learns rapidly (high $p_2$). When socialization is slow, more rapid learning by the code leads to greater knowledge at equilibrium; but when socialization is rapid, greater equilibrium knowledge is achieved through slower learning by the code. By far the highest equilibrium knowledge occurs when the code learns rapidly from individuals whose socialization to the code is slow.

The results pictured in Figure 1 confirm the observation that rapid learning is not always desirable (Herriott, Levinthal and March 1985; Lounamaa and March 1987).

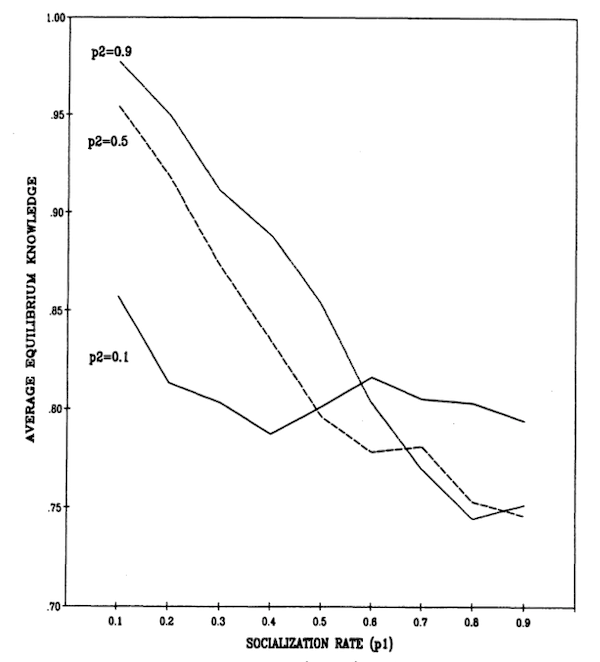
In previous work, it was shown that slower learning allows for greater exploration of possible alternatives and greater balance in the development of specialized competences. In the present model, a different version of the same general phenomenon is observed. The gains to individuals from adapting rapidly to the code (which is consistently closer to reality than the average individual) are offset by second-order losses stemming from the fact that the code can learn only from individuals who deviate from it. Slow learning on the part of individuals maintains diversity longer, thereby providing the exploration that allows the knowledge found in the organizational code to improve.

Effects of learning rate heterogeneity. The fact that fast individual learning from the code tends to have a favorable first-order effect on individual knowledge but an adverse effect on improvement in organizational knowledge and thereby on long-term individual improvement suggests that there might be some advantage to having a mix of fast and slow learners in an organization. Suppose the population of individuals in an organization is divided into two groups, one consisting of individuals who learn rapidly from the code ($p_1 = 0.9$) and the other consisting of individuals who learn slowly ($p_1 = 0.1$).

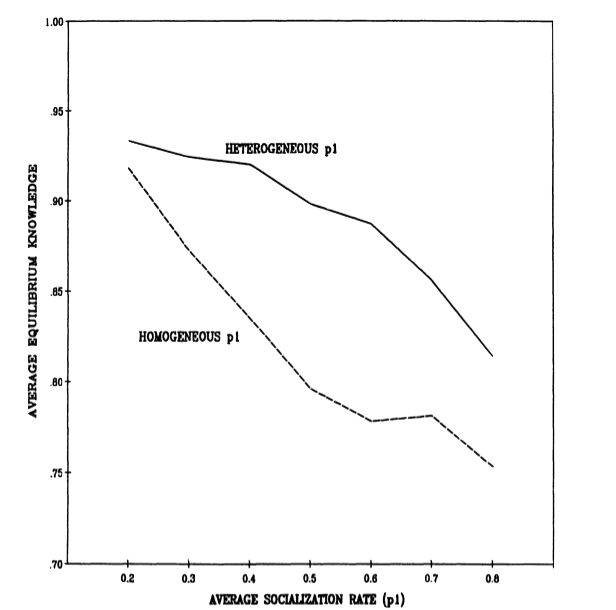
If an organization is partitioned into two groups in this way, the mutual learning process achieves an equilibrium in which all individuals and the code share the same beliefs. As would be expected from the results above with respect to homogeneous socialization rates, larger fractions of fast learners result in the process reaching equilibrium faster and in lower levels of knowledge at equilibrium than do smaller fractions of fast learners. However, as Figure 2 shows, for any average rate of learning from the code, it is better from the point of view of equilibrium knowledge to have that average reflect a mix of fast and slow learners rather than a homogeneous population. For equivalent average values of the socialization learning parameter ($p_1$), the heterogeneous population consistently produces higher equilibrium knowledge.

On the way to equilibrium, the knowledge gains from variability are disproportionately due to contributions by slow learners, but they are disproportionately realized (in their own knowledge) by fast learners. Figure 3 shows the effects on period-20 knowledge of varying the fraction of the population of individuals who are fast learners ($p_1 = 0.9$) rather than slow learners ($p_1 = 0.1$). Prior to reaching equilibrium, individuals with a high value for $p_1$, gain from being in an organization in which there are individuals having a low value for $p_1$, but the converse is not true.

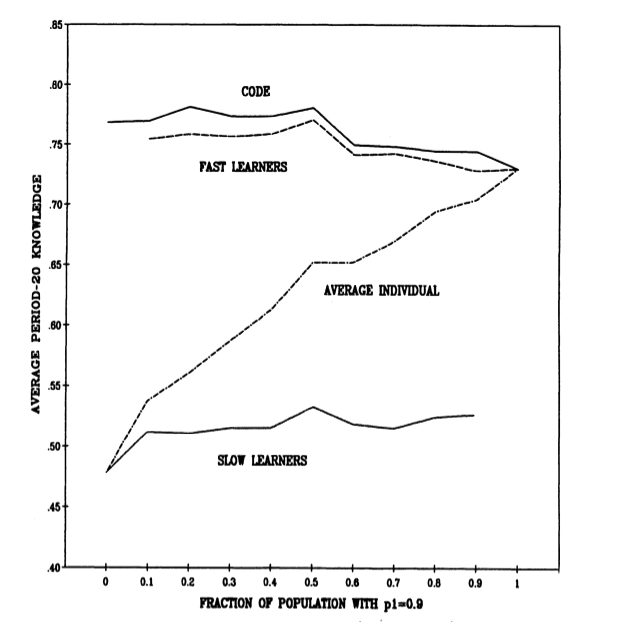
These results indicate that the fraction of slow learners in an organization is a significant factor in organizational learning. In the model, that fraction is treated as a parameter. Disparities in the returns to the two groups and their interdependence make optimizing with respect to the fraction of slow learners problematic if the rates of individual learning are subject to individual control. Since there are no obvious individual incentives for learning slowly in a population in which others are learning rapidly, it may be difficult to arrive at a fraction of slow learners that is optimal from the point of view of the code if learning rates are voluntarily chosen by individuals.

Basic Properties of the Model in a More Open System

These results can be extended by examining some alternative routes to selective slow learning in a somewhat more open system. Specifically, the role of turnover in the organization and turbulence in the environment are considered. In the case of turnover, organizational membership is treated as changing. In the case of turbulence, environmental reality is treated as changing.

Effects of personnel turnover. In the previous section, it was shown that variability is sustained by low values of $p_1$. Slow learners stay deviant long enough for the code to learn from them. An alternative way of producing variability in an organization is to introduce personnel turnover. Suppose that each time period each individual has a probability, $p_3$, of leaving the organization and being replaced by a new individual with a set of naive beliefs described by an m-tuple, having values equal to 1, 0, or —1, with equal probabilities. As might be expected, there is a consistent negative first-order effect of turnover on average individual knowledge. Since there is a positive relation between length of service in the organization and individual knowledge, the greater the turnover, the shorter the average length of service and the lower the average individual knowledge at any point. This effect is strong.

The effect of turnover on the organizational code is more complicated and reflects a trade-off between learning rate and turnover rate. Figure 4 shows the period-20 results for two different values of the socialization rate ($p_1$). If $p_1$, is relatively low, period-20 code knowledge declines with increasing turnover. The combination of slow learning and rapid turnover leads to inadequate exploitation. However, if $p_1$, is relatively high, moderate amounts of turnover improve the organizational code. Rapid socialization of individuals into the procedures and beliefs of an organization tends to reduce exploration. A modest level of turnover, by introducing less socialized people, increases exploration, and thereby improves aggregate knowledge. The level of knowledge reflected by the organizational code is increased, as is the average individual knowledge of those individuals who have been in the organization for some time. Note that this effect does not come from the superior knowledge of the average new recruit. Recruits are, on average, less knowledgeable than the individuals they replace. The gains come from their diversity.

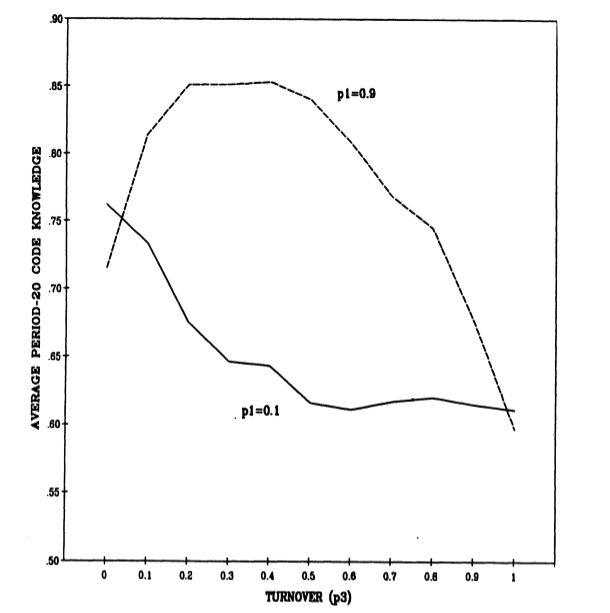
Turnover, like heterogeneity in learning rates, produces a distribution problem. Contributions to improving the code (and subsequently individual knowledge) come from the occasional newcomers who deviate from the code in a favorable way. Old-timers, on average, know more, but what they know is redundant with knowledge already reflected in the code. They are less likely to contribute new knowledge on the margin. Novices know less on average, but what they know is less redundant with the code and occasionally better, thus more likely to contribute to improving the code.

Effects of environmental turbulence. Since learning processes involve lags in adjustment to changes, the contribution of learning to knowledge depends on the amount of turbulence in the environment. Suppose that the value of any given dimension of reality shifts (from 1 to —1 or —1 to 1) in a given time period with probability $p_4$.

This captures in an elementary way the idea that understanding the world may be complicated by turbulence in the world. Exogenous environmental change makes adaptation essential, but it also makes learning from experience difficult (Weick 1979). In the model, the level of knowledge achieved in a particular (relatively early) time period decreases with increasing turbulence.

In addition, mutual learning has a dramatic long-run degenerate property under conditions of exogenous turbulence. As the beliefs of individuals and the code converge, the possibilities for improvement in either decline. Once a knowledge equilibrium is achieved, it is sustained indefinitely. The beliefs reflected in the code and those held by all individuals remain identical and unchanging, regardless of changes in reality. Even before equilibrium is achieved, the capabilities for change fall below the rate of change in the environment. As a result, after an initial period of increasing accuracy, the knowledge of the code and individuals is systematically degraded through changes in reality. Ultimately, the accuracy of belief reaches chance (i.e., where a random change in reality is as likely to increase accuracy of beliefs as it is to decrease it). The process becomes a random walk.

The degeneracy is avoided if there is turnover. Figure 5 plots the average level of code knowledge over time under conditions of turbulence ($p_4$ = 0.02). Two cases of learning are plotted, one without turnover ($p_3$ = 0), the other with moderate turnover ($p_3$ = 0.1). Where there is turbulence without turnover, code knowledge first rises to a moderate level, and then declines to 0, from which it subsequently wanders randomly. With turnover, the degeneracy is avoided and a moderate level of code knowledge is sustained in the face of environmental change. The positive effects of moderate turnover depend, of course, on the rules for selecting new recruits. In the present case, recruitment is not affected by the code. Replacing departing individuals with recruits closer to the current organizational code would significantly reduce the efficiency of turnover as a source of exploration.

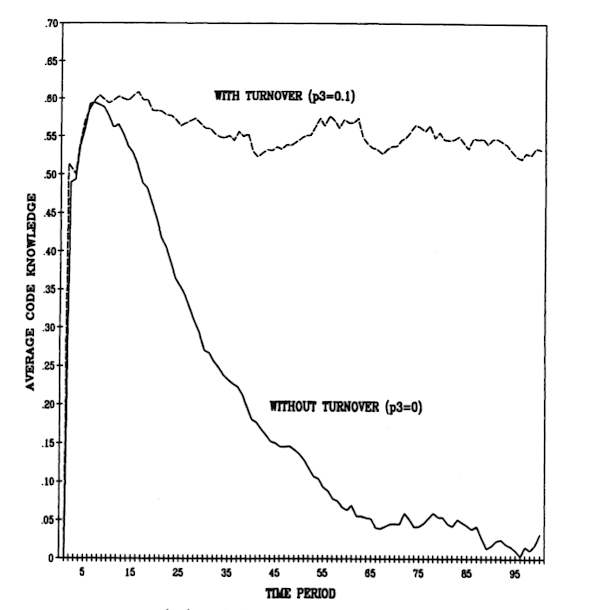
Turnover is useful in the face of turbulence, but it produces a disparity between code knowledge and the average knowledge of individuals in the organization. As a result, the match between turnover rate and level of turbulence that is desirable from the point of view of the organization’s knowledge is not necessarily desirable from the point of view of the knowledge of every individual in it, or individuals on average. In particular, where there is turbulence, there is considerable individual advantage to having tenure in an organization that has turnover. This seems likely to produce pressures by individuals to secure tenure for themselves while restricting it for others.

Knowledge and Ecologies of Competition

The model in the previous section examines one aspect of the social context of adaptation in organizations, the ways in which individual beliefs and an organizational code draw from each other over time. A second major feature of the social context of organizational learning is the competitive ecology within which learning occurs and knowledge is used. External competitive processes pit organizations against each other in pursuit of scarce environmental resources and opportunities. Examples are competition among business firms for customers and governmental subsidies. Internal competitive processes pit individuals in the organization against each other in competition for scarce organizational resources and opportunities. Examples are competition among managers for internal resources and hierarchical promotion. In these ecologies of competition, the competitive consequences of learning by one organization depend on learning by other organizations. In this section, these links among learning, performance, and position in an ecology of competition are discussed by considering some ways in which competitive advantage is affected by the accumulation of knowledge.

Competition and the Importance of Relative Performance

Suppose that an organization’s realized performance on a particular occasion is a draw from a probability distribution that can be characterized in terms of some measure of average value (x) and some measure of variability (v). Knowledge, and the learning process that produces it, can be described in terms of their effects on these two measures. A change in an organization’s performance distribution that increases average performance (i.e., makes x’ > x) will often be beneficial to an organization, but such a result is not assured when relative position within a group of competing organizations is important. Where returns to one competitor are not strictly determined by that competitor’s own performance but depend on the relative standings of the competitors, returns to changes in knowledge depend not only on the magnitude of the changes in the expected value but also on changes in variability and on the number of competitors.

To illustrate the phenomenon, consider the case of competition for primacy between a reference organization and N other organizations, each having normal performance distributions with mean = x and variance = v. The chance of the reference organization having the best performance within a group of identical competitors is 1/(N + 1). We compare this situation to one in which the reference organization has a normal performance distribution with mean = x’ and variance = v’. We evaluate the probability, P*, that the (x’, v’) organization will outperform all of the N (x,v) organizations. A performance distribution with a mean of x’ and a variance of v’ provides a competitive advantage in a competition for primacy if P* is greater than 1/(N + 1). It results in a competitive disadvantage if P* is less than 1/(N + 1).

If an organization faces only one competitor (N = 1), it is easy to see that any advantage in mean performance on the part of the reference organization makes P* greater than 1/(N + 1) = 0.5, regardless of the variance. Thus, in bilateral competition involving normal performance distributions, learning that increases the mean always pays off, and changes in the variance—whether positive or negative—have no effect.

The situation changes as N increases. Figure 6 shows the competitive success (failure) of an organization having a normal performance distribution with a mean = x’ and a variance = v’, when that organization is faced with N identical and independent competitors whose performance distributions are normal with mean = 0 and variance = 1. Each point in the space in Figure 6 represents a different possible normal performance distribution (x’,v’). Each line in the figure is associated with a particular N and connects the (x’, v’) pairs for which P* = 1/(N + 1). The lines are constructed by estimating, for each value of v’ from 0 to 2 in steps of 0.05, the value of x’ for which p* = 1/(N + 1). Each estimate is based on 5000 simulations. Since if x’ = 0 and v’ = 1, P* = 1/(N + 1) for any N, each of the lines is constrained to pass through the (0, 1) point. The area to the right and above a line includes (x’, v’) combinations for which P* is greater than 1/(N + 1), thus that yield a competitive advantage relative to (0, 1). The area to the left and below a line includes (x’,v’) combinations for which P* is less than 1/(N + 1), thus that yield a competitive disadvantage relative to (0, 1).

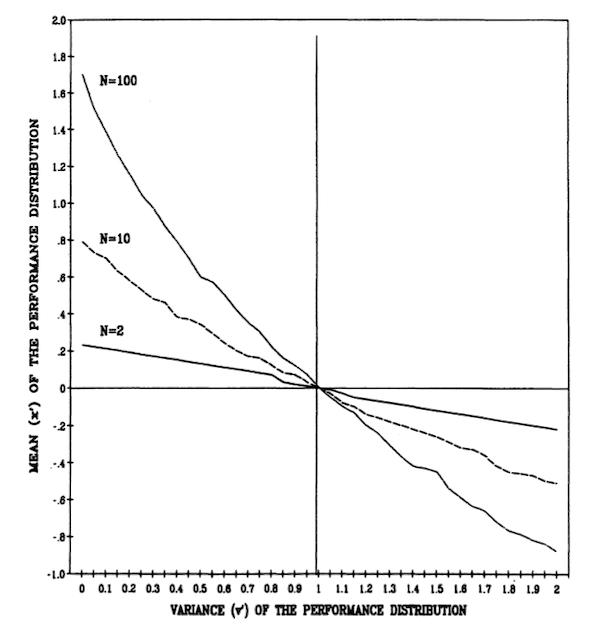
The pattern is clear. If N is greater than 1 (but finite), increases in either the mean or the variance have a positive effect on competitive advantage, and sufficiently large increases in either can offset decreases in the other. The trade-off between increases in the mean and increases in the variance is strongly affected by N. As the number of competitors increases, the contribution of the variance to competitive advantage increases until at the limit, as N goes to infinity, the mean becomes irrelevant.

Learning, Knowledge, and Competitive Advantage

The effects of learning are realized in changes in the performance distribution. The analysis indicates that if learning increases both the mean and the variance of a normal performance distribution, it will improve competitive advantage in a competition for primacy. The model also suggests that increases in the variance may compensate for decreases in the mean; decreases in the variance may nullify gains from increases in the mean. These variance effects are particularly significant when the number of competitors is large.

The underlying argument does not depend on competition being only for primacy. Such competition is a special case of competition for relative position. The general principle that relative position is affected by variability, and increasingly so as the number of competitors increases, is true for any position. In competition to achieve relatively high positions, variability has a positive effect. In competition to avoid relatively low positions, variability has a negative effect.

Nor does the underlying argument depend on the assumption of normality or other symmetry in the performance distributions. Normal performance distributions are special cases in which the tails of the distribution are specified when the mean and variance are specified. For general distributions, as the number of competitors increases, the likelihood of finishing first depends increasingly on the right-hand tail of the performance distribution, and the likelihood of finishing last depends increasingly on the left-hand tail (David 1981). If learning has different effects on the two tails of the distribution, the right-hand tail effect will be such more important in competition for primacy among many competitors. The left-hand tail will be much more important in competition to avoid finishing last.

Some learning processes increase both average performance and variability. A standard example would be the short-run consequences from adoption of a new technology. If a new technology is so clearly superior as to overcome the disadvantages of unfamiliarity with it, it will offer a higher expected value than the old technology. At the same time, the limited experience with the new technology (relative to experience with the old) will lead to an increased variance. A similar result might be expected with the introduction of a new body of knowledge or new elements of cultural diversity to an organization, for example, through the introduction of individuals with untypical skills, attitudes, ethnicity, or gender.

Learning processes do not necessarily lead to increases in both average performance and variation, however. Increased knowledge seems often to reduce the variability of performance rather than to increase it. Knowledge makes performance more reliable. As work is standardized, as techniques are learned, variability, both in the time required to accomplish tasks and in the quality of task performance, is reduced. Insofar as that increase is reliability comes from a reduction in the left-hand tail, the likelihood of finishing last in a competition among many is reduced without changing the likelihood of finishing first. However, if knowledge has the effect of reducing the right-hand tail of the distribution, it may easily decrease the chance of being best among several competitors even though it also increases average performance. The question is whether you can do exceptionally well, as opposed to better than average, without leaving the confines of conventional action. The answer is complicated, for it depends on a more careful specification of the kind of knowledge involved and its precise effects on the right-hand tail of the distribution. But knowledge that simultaneously increases average performance and its reliability is not a guarantee of competitive advantage.

Consider, for example, the case of modern information and decision technology based on computers. In cases where time is particularly important, information technology has a major effect on the mean, less on the variance. Some problems in environmental scanning for surprises, changes, or opportunities probably fall into such a category. Under such conditions, appropriate use of information technology seems likely to improve competitive position. On the other hand, in many situations the main effect of information technology is to make outcomes more reliable. For example, additional data, or more detailed analyses, seem likely to increase reliability in decisions more rapidly than they will increase their average returns. In such cases, the effects on the tails are likely to dominate the effects on the mean. The net effect of the improved technology on the chance of avoiding being the worst competitor will be positive, but the effect on the chance of finishing at the head of the pack may well be negative.

Similarly, multiple independent projects may have an advantage over a single, coordinated effort. The average result from independent projects is likely to be lower than that realized from a coordinated one, but their right-hand side variability can compensate for the reduced mean in a competition for primacy. The argument can be extended more generally to the effects of close collaboration or cooperative information exchange. Organizations that develop effective instruments of coordination and communication probably can be expected to do better (on average) than those that are more loosely coupled, and they also probably can be expected to become more reliable, less likely to deviate significantly from the mean of their performance distributions. The price of reliability, however, is a smaller chance of primacy among competitors.

Competition for Relative Position and Strategic Action

The arguments above assume that the several individual performances of competitors are independent draws from a distribution of possible performances, and that the distribution cannot be arbitrarily chosen by the competitors. Such a perspective is incomplete. It is possible to see both the mean and the reliability of a performance distribution (at least partially) as choices made strategically. In the long run, they represent the result of organizational choices between investments in learning and in consumption of the fruits of current capabilities, thus the central focus of this paper. In the short run, the choice of mean can be seen as a choice of effort or attention. By varying effort, an organization selects a performance mean between an entitlement (zero-effort) and a capability (maximum-effort) level. Similarly, in the short run, variations in the reliability of performance can be seen as choices of knowledge or risk that can be set willfully within the range of available alternatives.

These choices, insofar as they are made rationally, will not, in general, be independent of competition. If relative position matters, as the number of competitors increases, strategies for increasing the mean through increased effort or greater knowledge become less attractive relative to strategies for increasing variability. In the more general situation, suppose organizations face competition from numerous competitors who vary in their average capabilities but who can choose their variances. If payoffs and preferences are such that finishing near the top matters a great deal, those organizations with performance distributions characterized by comparatively low means will (if they can) be willing to sacrifice average performance in order to augment the right-hand tails of their performance distributions. In this way, they improve their chances of winning, thus force their more talented competitors to do likewise, and thereby convert the competition into a right-hand tail “race” in which average performance (due to ability and effort) becomes irrelevant. These dynamics comprise powerful countervailing forces to the tendency for experience to eliminate exploration and are a reminder that the learning dominance of exploitation is, under some circumstances, constrained not only by slow learning and turnover but also by reason.

Little Models and Old Wisdom

Learning, analysis, imitation, regeneration, and technological change are major components of any effort to improve organizational performance and strengthen competitive advantage. Each involves adaptation and a delicate trade-off between exploration and exploitation. The present argument has been that these trade-offs are affected by their contexts of distributed costs and benefits and ecological interaction. The essence of exploitation is the refinement and extension of existing competences, technologies, and paradigms. Its returns are positive, proximate, and predictable. The essence of exploration is experimentation with new alternatives. Its returns are uncertain, distant, and often negative. Thus, the distance in time and space between the locus of learning and the locus for the realization of returns is generally greater in the case of exploration than in the case of exploitation, as is the uncertainty.

Such features of the context of adaptation lead to a tendency to substitute exploitation of known alternatives for the exploration of unknown ones, to increase the reliability of performance rather more than its mean. This property of adaptive processes is potentially self-destructive. As we have seen, it degrades organizational learning in a mutual learning situation. Mutual learning leads to convergence between organizational and individual beliefs. The convergence is generally useful both for individuals and for an organization. However, a major threat to the effectiveness of such learning is the possibility that individuals will adjust to an organizational code before the code can learn from them. Relatively slow socialization of new organizational members and moderate turnover sustain variability in individual beliefs, thereby improving organizational and average individual knowledge in the long run.

An emphasis on exploitation also compromises competitive position where finishing near the top is important. Knowledge-based increases in average performance can be insufficient to overcome the adverse effects produced by reductions in variability. The ambiguous usefulness of learning in a competitive race is not simply an artifact of representing knowledge in terms of the mean and variance of a normal distribution. The key factor is the effect of knowledge on the right-hand tail of the performance distribution. Thus, in the end, the effects stem from the relation between knowledge and discovery. Michael Polanyi, commenting on one of his contributions to physics, observed (Polanyi 1963, p. 1013) that “I would never have conceived my theory, let alone have made a great effort to verify it, if I had been more familiar with major developments in physics that were taking place. Moreover, my initial ignorance of the powerful, false objections that were raised against my ideas protected those ideas from being nipped in the bud.”

These observations do not overturn the renaissance. Knowledge, learning, and education remain as profoundly important instruments of human well-being. At best, the models presented here suggest some of the considerations involved in thinking about choices between exploration and exploitation and in sustaining exploration in the face of adaptive processes that tend to inhibit it. The complexity of the distribution of costs and returns across time and groups makes an explicit determination of optimality a nontrivial exercise. But it may be instructive to reconfirm some elements of folk wisdom asserting that the returns to fast learning are not all positive, that rapid socialization may hurt the socializers even as it helps the socialized, that the development of knowledge may depend on maintaining an influx of the naive and ignorant, and that competitive victory does not reliably go to the properly educated.