The Strength of Weak Ties

Abstract

Analysis of social networks is suggested as a tool for linking micro and macro levels of sociological theory. The procedure is illustrated by elaboration of the macro implications of one aspect of small-scale interaction: the strength of dyadic ties. It is argued that the degree of overlap of two individuals’ friendship networks varies directly with the strength of their tie to one another. The impact of this principle on diffusion of influence and information, mobility opportunity, and community organization is explored. Stress is laid on the cohesive power of weak ties. Most network models deal, implicitly, with strong ties, thus confining their applicability to small, well- defined groups. Emphasis on weak ties lends itself to discussion of relations between groups and to analysis of segments of social structure not easily defined in terms of primary groups.

Introduction

A fundamental weakness of current sociological theory is that it does not relate micro-level interactions to macro-level patterns in any convincing way. Large-scale statistical, as well as qualitative, studies offer a good deal of insight into such macro phenomena as social mobility, community organization, and political structure. At the micro level, a large and increasing body of data and theory offers useful and illuminating ideas about what transpires within the confines of the small group. But how interaction in small groups aggregates to form large-scale patterns eludes us in most cases.

I will argue, in this paper, that the analysis of processes in interpersonal networks provides the most fruitful micro-macro bridge. In one way or another, it is through these networks that small-scale interaction becomes translated into large-scale patterns, and that these, in turn, feed back into small groups.

Sociometry, the precursor of network analysis, has always been curiously peripheral—invisible, really—in sociological theory. This is partly because it has usually been studied and applied only as a branch of social psychology; it is also because of the inherent complexities of precise network analysis. We have had neither the theory nor the measurement and sampling techniques to move sociometry from the usual small-group level to that of larger structures. While a number of stimulating and suggestive studies have recently moved in this direction (Bott 1957; Mayer 1961; Milgram 1967; Boissevain 1968; Mitchell 1969), they do not treat structural issues in much theoretical detail. Studies which do so usually involve a level of technical complexity appropriate to such forbidding sources as the Bulletin of Mathematical Biophysics, where the original motivation for the study of networks was that of developing a theory of neural, rather than social, interaction (see the useful review of this literature by Coleman [1960]; also Rapoport [1963]).

The strategy of the present paper is to choose a rather limited aspect of small-scale interaction—the strength of interpersonal ties—and to show, in some detail, how the use of network analysis can relate this aspect to such varied macro phenomena as diffusion, social mobility, political organization, and social cohesion in general. While the analysis is essentially qualitative, a mathematically inclined reader will recognize the potential for models; mathematical arguments, leads, and references are suggested mostly in footnotes.

The Strength of Ties

Most intuitive notions of the “strength” of an interpersonal tie should be satisfied by the following definition: the strength of a tie is a (probably linear) combination of the amount of time, the emotional intensity, the intimacy (mutual confiding), and the reciprocal services which characterize the tie Ties discussed in this paper are assumed to be positive and symmetric; a comprehensive theory might require discussion of negative and/or asymmetric ties, but this would add unnecessary complexity to the present, exploratory comments.. Each of these is somewhat independent of the other, though the set is obviously highly intracorrelated. Discussion of operational measures of and weights attaching to each of the four elements is postponed to future empirical studies. Some anthropologists suggest “multiplexity,” that is, multiple contents in a relationship, as indicating a strong tie (Kapferer 1969, p. 213). While this may be accurate in some circumstances, ties with only one content or with diffuse content may be strong as well (Simmel 1950, pp. 317-29). The present definition would show most multiplex ties to be strong but also allow for other possibilities. It is sufficient for the present purpose if most of us can agree, on a rough intuitive basis, whether a given tie is strong, weak, or absent. Included in “absent” are both the lack of any relationship and ties without substantial significance, such as a “nodding” relationship between people living on the same street, or the “tie” to the vendor from whom one customarily buys a morning newspaper. That two people “know” each other by name need not move their relation out of this category if their interaction is negligible. In some contexts, however (disasters, for example), such “negligible” ties might usefully be distinguished from the absence of one. This is an ambiguity caused by substitution, for convenience of exposition, of discrete values for an underlying continuous variable.

Consider, now, any two arbitrarily selected individuals—call them A and B—and the set, S=C,D,E,…, of all persons with ties to either or both of them. In Barnes’s terminology, the union of their respective primary stars (1969, p. 58). The hypothesis which enables us to relate dyadic ties to larger structures is: the stronger the tie between A and B, the larger the proportion of individuals in S to whom they will both be tied, that is, connected by a weak or strong tie. This overlap in their friendship circles is predicted to be least when their tie is absent, most when it is strong, and intermediate when it is weak.

The proposed relationship results, first, from the tendency (by definition) of stronger ties to involve larger time commitments. If A-B and A-C ties exist, then the amount of time C spends with B depends (in part) on the amount A spends with B and C, respectively. (If the events “A is with B” and “A is with C” were independent, then the event “C is with A and B” would have probability equal to the product of their probabilities. For example, if A and B are together 60% of the time, and A and C 40%, then C, A, and B would be together 24% of the time. Such independence would be less likely after than before B and C became acquainted.) If C and B have no relationship, common strong ties to A will probably bring them into interaction and generate one. Implicit here is Homans’s idea that “the more frequently persons interact with one another, the stronger their sentiments of friendship for one another are apt to be” (1950, p. 133).

The hypothesis is made plausible also by empirical evidence that the stronger the tie connecting two individuals, the more similar they are, in various ways (Berscheid and Walster 1969, pp. 69-91; Bramel 1969, pp. 9-16; Brown 1965, pp. 71-90; Laumann 1968; Newcomb 1961, chap. 5; Precker 1952). Thus, if strong ties connect A to B and A to C, both C and B, being similar to A, are probably similar to one another, increasing the likelihood of a friendship once they have met. Applied in reverse, these two factors—time and similarity—indicate why weaker A-B and A-C ties make a C-B tie less likely than strong ones: C and B are less likely to interact and less likely to be compatible if they do.

The theory of cognitive balance, as formulated by Heider (1958) and especially by Newcomb (1961, pp. 4-23), also predicts this result. If strong ties A-B and A-C exist, and if B and C are aware of one another, anything short of a positive tie would introduce a “psychological strain” into the situation since C will want his own feelings to be congruent with those of his good friend, A, and similarly, for B and his friend, A. Where the ties are weak, however, such consistency is psychologically less crucial. (On this point see also Homans [1950, p. 255] and Davis [1963, p. 448].)

Some direct evidence for the basic hypothesis exists (Kapferer 1969, p. 229 n.; Laumann and Schuman 1967; Rapoport and Horvath 1961; Rapoport 1963). The models and experiments of Rapoport and his associates have been a major stimulus to this paper. In 1954 he commented on the “well-known fact that the likely contacts of two individuals who are closely acquainted tend to be more overlapping than those of two arbitrarily selected individuals” (p. 75). His and Horvath’s 1961 hypothesis is even closer to mine: “one would expect the friendship relations, and therefore the overlap bias of the acquaintance circles, to become less tight with increasing numerical rank-order” (p. 290). (i.e., best friend, second-best friend, third-best, etc.) Their development of this hypothesis, however, is quite different, substantively and mathematically, from mine (Rapoport 1953a, 1953b, 1954, 1963; Rapoport and Horvath 1961). This evidence is less comprehensive than one might hope. In addition, however, certain inferences from the hypothesis have received empirical support. Description of these inferences will suggest some of the substantive implications of the above argument.

Weak Ties in Diffusion Process

To derive implications for large networks of relations, it is necessary to frame the basic hypothesis more precisely. This can be done by investigating the possible triads consisting of strong, weak, or absent ties among A, B, and any arbitrarily chosen friend of either or both (i.e., some member of the set S, described above). A thorough mathematical model would do this in some detail, suggesting probabilities for various types. This analysis becomes rather involved, however, and it is sufficient for my purpose in this paper to say that the triad which is most unlikely to occur, under the hypothesis stated above, is that in which A and B are strongly linked, A has a strong tie to some friend C, but the tie between C and B is absent. This triad is shown in figure 1. To see the consequences of this assertion, I will exaggerate it in what follows by supposing that the triad shown never occurs—that is, that the B-C tie is always present (whether weak or strong), given the other two strong ties. Whatever results are inferred from this supposition should tend to occur in the degree that the triad in question tends to be absent.

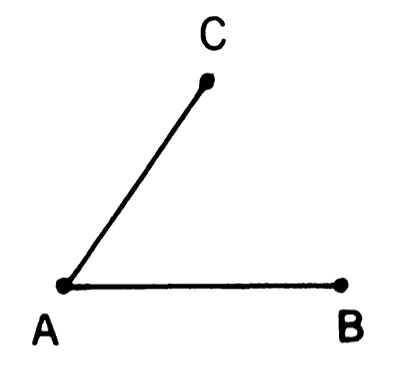
Some evidence exists for this absence. Analyzing 651 sociograms, Davis (1970, p. 845) found that in 90% of them triads consisting of two mutual choices and one nonchoice occurred less than the expected random number of times. If we assume that mutual choice indicates a strong tie, this is strong evidence in the direction of my argument. This assumption is suggested by one of Davis’s models (1970, p. 846) and made explicitly by Mazur (1971). It is not obvious, however. In a free-choice sociometric test or a fixed-choice one with a large number of choices, most strong ties would probably result in mutual choice, but some weak ones might as well. With a small, fixed number of choices, most mutual choices should be strong ties, but some strong ties might show up as asymmetric. For a general discussion of the biases introduced by sociometric procedures, see Holland and Leinhardt (1971b). Newcomb (1961, pp. 160- 65) reports that in triads consisting of dyads expressing mutual “high attraction,” the configuration of three strong ties became increasingly frequent as people knew one another longer and better; the frequency of the triad pictured in figure 1 is not analyzed, but it is implied that processes of cognitive balance tended to eliminate it.

The significance of this triad’s absence can be shown by using the concept of a “bridge”; this is a line in a network which provides the only path between two points (Harary, Norman, and Cartwright 1965, p. 198). Since, in general, each person has a great many contacts, a bridge between A and B provides the only route along which information or influence can flow from any contact of A to any contact of B, and, consequently, from anyone connected indirectly to A to anyone connected indirectly to B. Thus, in the study of diffusion, we can expect bridges to assume an important role.

Now, if the stipulated triad is absent, it follows that, except under unlikely conditions, no strong tie is a bridge. Consider the strong tie A-B: if A has another strong tie to C, then forbidding the triad of figure 1 implies that a tie exists between C and B, so that the path A-C-B exists between A and B; hence, A-B is not a bridge. A strong tie can be a bridge, therefore, only if neither party to it has any other strong ties, unlikely in a social network of any size (though possible in a small group). Weak ties suffer no such restriction, though they are certainly not automatically bridges. What is important, rather, is that all bridges are weak ties.

In large networks it probably happens only rarely, in practice, that a specific tie provides the only path between two points. The bridging function may nevertheless be served locally. In figure 2a, for example, the tie A-B is not strictly a bridge, since one can construct the path A-E-J-B (and others). Yet, A-B is the shortest route to B for F, D, and C. This function is clearer in figure 2b. Here, A-B is, for C, D, and others, not only a local bridge to B, but, in most real instances of diffusion, a much more likely and efficient path. Harary et al. point out that “there may be a distance [length of path] beyond which it is not feasible for $u$ to communicate with $v$ because of costs or distortions entailed in each act of transmission. If $v$ does not lie within this critical distance, then he will not receive messages originating with $u$ (1965, p. 159). I will refer to a tie as a “local bridge of degree $n$” if $n$ represents the shortest path between its two points (other than itself), and $n$ > 2. In figure 2a, A-B is a local bridge of degree 3, in 2b, of degree 13. As with bridges in a highway system, a local bridge in a social network will be more significant as a connection between two sectors to the extent that it is the only alternative for many people—that is, as its degree increases. A bridge in the absolute sense is a local one of infinite degree. By the same logic used above, only weak ties may be local bridges.

Suppose, now, that we adopt Davis’s suggestion that “in interpersonal flows of most any sort the probability that ‘whatever it is’ will flow from person $i$ to person $j$ is (a) directly proportional to the number of all-positive (friendship) paths connecting $i$ and $j$; and (b) inversely proportional to the length of such paths” (1969, p. 549). Though this assumption seems plausible, it is by no means self-evident. Surprisingly little empirical evidence exists to support or refute it. The significance of weak ties, then, would be that those which are local bridges create more, and shorter, paths. Any given tie may, hypothetically, be removed from a network; the number of paths broken and the changes in average path length resulting between arbitrary pairs of points (with some limitation on length of path considered) can then be computed. The contention here is that removal of the average weak tie would do more “damage” to transmission probabilities than would that of the average strong one. In a more comprehensive treatment it would be useful to consider to what extent a set of weak ties may be considered to have bridging functions. This generalization requires a long, complex discussion and is not attempted here (see Harary et al. 1965, pp. 211-16).

Intuitively speaking, this means that whatever is to be diffused can reach a larger number of people, and traverse greater social distance (i.e., path length), We may define the “social distance” between two individuals in a network as the number of lines in the shortest path from one to another. This is the same as the definition of “distance” between points in graph theory (Harary et al. 1965, pp. 32-33, 138-41). The exact role of this quantity in diffusion and epidemic theory is discussed by Solomonoff and Rapoport (1951). when passed through weak ties rather than strong. If one tells a rumor to all his close friends, and they do likewise, many will hear the rumor a second and third time, since those linked by strong ties tend to share friends. If the motivation to spread the rumor is dampened a bit on each wave of retelling, then the rumor moving through strong ties is much more likely to be limited to a few cliques than that going via weak ones; bridges will not be crossed. If a damping effect is not specified, the whole population would hear the rumor after a sufficiently large number of retellings, since few real networks include totally self-contained cliques. The effective difference between using weak and strong ties, then, is one of people reached per unit of (ordinal) time. This could be called “velocity” of transmission. I am indebted to Scott Feld for this point.

Since sociologists and anthropologists have carried out many hundreds of diffusion studies—Rogers’s 1962 review dealt with 506—one might suppose that the above claims could easily be put to test. But this is not so, for several reasons. To begin with, though most diffusion studies find that personal contacts are crucial, many undertake no sociometric investigation. (Rogers [1962] discusses this point.) When sociometric techniques are used, they tend to discourage the naming of those weakly tied to the respondent by sharply limiting the numbers of choices allowed. Hence, the proposed importance of weak ties in diffusion is not measured. Even when more sociometric information is collected there is almost never an attempt to directly retrace the exact interpersonal paths traversed by an (idea, rumor, or) innovation. More commonly, the time when each individual adopted the innovation is recorded, as is the number of sociometric choices he received from others in the study. Those receiving many choices are characterized as “central,” those with few as “marginal”; this variable is then correlated with time of adoption and inferences made about what paths were probably followed by the innovation.

One point of controversy in diffusion studies can be related to my argument. Some have indicated that early innovators are marginal, that they “underconform to norms to such a degree that they are perceived as highly deviant” (Rogers 1962, p. 197). Others (e.g., Coleman, Katz, and Menzel [1966] on the adoption of a new drug by doctors) find that those named more frequently adopt an innovation substantially earlier. Becker (1970) tries to resolve the question of whether early innovators are “central” or “marginal” by referring to the “perceived risks of adoption of a given innovation.” His study of public health innovations shows that when a new program is thought relatively safe and uncontroversial (as with the drug of Coleman et al.), central figures lead in its adoption; otherwise, marginal ones do (p. 273). He explains the difference in terms of a greater desire of “central” figures to protect their professional reputation.

Kerckhoff, Back, and Miller (1965) reach a similar conclusion in a different type of study. A Southern textile plant had been swept by “hysterical contagion”: a few, then more and more workers, claiming bites from a mysterious ‘insect,’ became nauseous, numb, and weak, leading to a plant shutdown. When the affected workers were asked to name their three best friends, many named one another, but the very earliest to be stricken were social isolates, receiving almost no choices. An explanation, compatible with Becker’s, is offered: since the symptoms might be thought odd, early “adopters” were likely to be found among the marginal, those less subject to social pressures. Later, “it is increasingly likely that some persons who are socially integrated will be affected. . . . The contagion enters social networks and is disseminated with increasing rapidity” (p. 13). This is consistent with Rogers’s comment that while the first adopters of innovations are marginal, the next group, “early adopters,” “are a more integrated part of the local social system than the innovators” (1962, p. 183).

“Central” and “marginal” individuals may well be motivated as claimed; but if the marginal are genuinely so, it is difficult to see how they can ever spread innovations successfully. We may surmise that since the resistance to a risky or deviant activity is greater than to a safe or normal one, a larger number of people will have to be exposed to it and adopt it, in the early stages, before it will spread in a chain reaction. Individuals with many weak ties are, by my arguments, best placed to diffuse such a difficult innovation, since some of those ties will be local bridges. These individuals are what is often called, in organizational analysis, “liaison persons,” though their role here is different from the one usually discussed. (Cf. the concept in graph theory of a “cut point”—one which, if removed from a graph, disconnects one part from another [Harary 1965].) In general, a bridge has one liaison person on each side, but the existence of a liaison person does not imply that of a bridge. For local bridges, the concept of local liaisons could be developed. In a more microscopically oriented discussion I would devote more time to the liaison role. For now, I only point out that, under the present assumptions, one can be a liaison between two network sectors only if all his ties into one or both are weak. An initially unpopular innovation spread by those with few weak ties is more likely to be confined to a few cliques, thus being stillborn and never finding its way into a diffusion study.

That the “marginal” innovators of diffusion studies might actually be rich in weak ties is possible, given the usual sociometric technique, but in most cases this is purely speculative. Kerckhoff and Back, however, in a later more detailed analysis of the hysteria incident, indicate that besides asking about one’s “three best friends,” they also asked with whom workers ate, worked, shared car pools, etc. They report that five of the six workers earliest affected “are social isolates when friendship choices are used as the basis of analysis. Only 1 of the 6 is mentioned as a friend by anyone in our sample. This is made even more striking when we note that these 6 women are mentioned with considerable frequency when other bases for choice are used. In fact, they are chosen more frequently on a ‘non-friendship’ basis than are the women in any of the other categories” (1968, p. 112).

This finding lends credence to the weak-tie argument, but is inconclusive. A somewhat different kind of diffusion study offers more direct support: the “small-world” investigations of Milgram and his associates. The name of these studies stems from the typical comment of newly introduced individuals who discover some common acquaintance; this situation is generalized in an attempt to measure, for arbitrarily chosen pairs of individuals in the United States, how long a path of personal contacts would be needed to connect them. A booklet is given to randomly designated senders who are asked to forward it toward some named target person, via someone the sender knows personally who would be more likely than himself to know the target. The new recipient then advances the booklet similarly; eventually it reaches the target or someone fails to send it on. The proportion of such chains completed has ranged from 12% to 33% in different studies, and the number of links in completed chains has ranged from two to 10, averaging between five and eight (Milgram 1967; Travers and Milgram 1969; Korte and Milgram 1970).

Each time someone forwards a booklet he also sends a postcard to the researchers, indicating, among other things, the relationship between himself and the next receiver. Two of the categories which can be chosen are “friend” and ‘acquaintance.” I will assume that this corresponds to “strong” and “weak” ties. In one of the studies, white senders were asked to forward the booklet to a target who was Negro. In such chains, a crucial point was the first sending of the booklet from a white to a Negro. In 50% of the instances where the white described this Negro as an “acquaintance,” the chain was ultimately completed; completion rate fell to 26%, however, when the white sent the booklet to a Negro “friend.” (My computation, based on unpublished data kindly supplied by Charles Korte. See Korte [1967] and Korte and Milgram [1970].) Thus, weaker interracial ties can be seen to be more effective in bridging social distance.

Another relevant study, by Rapoport and Horvath (1961), is not exactly one of diffusion but is closely related in that it traces out paths along which diffusion could take place. They asked each individual in a Michigan junior high school (N = 851) to list his eight best friends in order of preference. Then, taking a number of random samples from the group (sample size, an arbitrary number, was nine), they traced out, for each sample, and averaged over all the samples, the total number of people reached by following along the network of first and second choices. That is, the first and second choices of each sample member were tabulated, then the first and second choices of these people were added in, etc., counting, at each remove, only names not previously chosen, and continuing until no new people were reached. The same procedure was followed using second and third choices, third and fourth, etc., up to seventh and eighth. (The theoretical connection of this tracing procedure to diffusion is discussed by Rapoport [1953a, 19530, and especially 1954].)

The smallest total number of people were reached through the networks generated by first and second choices—presumably the strongest ties—and the largest number through seventh and eighth choices. This corresponds to my assertion that more people can be reached through weak ties. A parameter in their mathematical model of the sociogram, designed to measure, approximately, the overlap of acquaintance circles, declined monotonically with increasing rank order of friends. This parameter, θ, measures such overlap in the following sense: it is zero in a random net—one in which individuals choose others at random—and is one in a net made up entirely of cliques disconnected each from every other. Intermediate values of θ, however, do not have a good intuitive interpretation in terms of individuals, but only with reference to the particular mathematical model defining the parameter; thus it does not correspond precisely to my arguments about friendship overlap.

Weak Ties in Egocentric Networks

In this section and the next, I want to discuss the general significance of the above findings and arguments at two levels: first that of individuals, then that of communities. These discussions make no pretense of being comprehensive; they are meant only to illustrate possible applications.

In recent years, a great deal of literature has appeared analyzing the impact on the behavior of individuals of the social networks in which they are imbedded. Some of the studies have emphasized the ways in which behavior is shaped and constrained by one’s network (Bott 1957; Mayer 1961; Frankenberg 1965), others the ways in which individuals can manipulate these networks to achieve specific goals (Mayer 1966; Boissevain 1968; Kapferer 1969). Both facets are generally supposed to be affected by the structure of one’s network. Bott argued that the crucial variable is that of whether one’s friends tend to know one another (“closeknit” network) or not (“loose-knit” network). Barnes makes this dichotomy into a continuous variable by counting the number of ties observed in the network formed by ego and his friends and dividing it by the ratio of possible ones; this then corresponds to what is often called network “density” (Barnes 1969; Tilly 1969). But if the crucial question is really whether ego’s friends know each other, this measure should probably be computed after ego and his ties have been subtracted from the network; distortions caused by failure to do so will be especially great in small networks. It is important to note, also, that in nonegocentric networks, there is no simple correspondence between density and any “average” measure of the extent to which the various egos have friends who know one another. “Density,” as used here, should not be confused with the “axone density” of Rapoport’s models—the number of choices issuing from each node of a network.

Epstein (1969) points out, however, that different parts of ego’s network may have different density. He calls those with whom one “interacts most intensely and most regularly, and who are therefore also likely to come to know one another,” the “effective network”; the “remainder constitute the extended network” (pp. 110-11). This is close to saying, in my terms, that one’s strong ties form a dense network, one’s weak ties a less dense one. I would add that one’s weak ties which are not local bridges might as well be counted with the strong ties, to maximize separation of the dense from the less dense network sectors.

One point on which there is no general agreement is whether ego’s network should be treated as composed only of those to whom he is tied directly, or should include the contacts of his contacts, and/or others. Analyses stressing encapsulation of an individual by his network tend to take the former position, those stressing manipulation of networks, the latter, since information or favors available through direct contacts may depend on who their contacts are. I would argue that by dividing ego’s network into that part made up of strong and nonbridging weak ties on the one hand, and that of bridging weak ties on the other, both orientations can be dealt with. Ties in the former part should tend to be to people who not only know one another, but who also have few contacts not tied to ego as well. In the “weak” sector, however, not only will ego’s contacts not be tied to one another, but they will be tied to individuals not tied to ego. Indirect contacts are thus typically reached through ties in this sector; such ties are then of importance not only in ego’s manipulation of networks, but also in that they are the channels through which ideas, influences, or information socially distant from ego may reach him. The fewer indirect contacts one has the more encapsulated he will be in terms of knowledge of the world beyond his own friendship circle; thus, bridging weak ties (and the consequent indirect contacts) are important in both ways.

I will develop this point empirically by citing some results from a labor-market study I have recently completed. Labor economists have long been aware that American blue-collar workers find out about new jobs more through personal contacts than by any other method. (Many studies are reviewed by Parnes 1954, chap. 5.) Recent studies suggest that this is also true for those in professional, technical, and managerial positions (Shapero, Howell, and Tombaugh 1965; Brown 1967; Granovetter 1970). My study of this question laid special emphasis on the nature of the tie between the job changer and the contact person who provided the necessary information.

In a random sample of recent professional, technical, and managerial job changers living in a Boston suburb, I asked those who found a new job through contacts how often they saw the contact around the time that he passed on job information to them. I will use this as a measure of tie strength. Although this corresponds only to the first of the four dimensions in my definition, supplementary anecdotal evidence from interviews makes it likely that, in this case, the entire definition is satisfied by this measure. At the time of research, it had not occurred to me that tie strength would be a useful variable. A natural a priori idea is that those with whom one has strong ties are more motivated to help with job information. Opposed to this greater motivation are the structural arguments I have been making: those to whom we are weakly tied are more likely to move in circles different from our own and will thus have access to information different from that which we receive.

I have used the following categories for frequency of contact: often = at least twice a week; occasionally = more than once a year but less than twice a week; rarely = once a year or less. Of those finding a job through contacts, 16.7% reported that they saw their contact often at the time, 55.6% said occasionally, and 27.8% rarely (N = 54). The numbers reported are small because they represent a random subsample of 100, who were interviewed personally, of the total sample of 282. The personal interview allowed more detailed questioning. Comparisons between the mail sample and the interview sample on the large number of items which were put to both show almost no significant differences; this suggests that results observed in the smaller sample on those items put to it alone would not be much different in the mail sample. The skew is clearly to the weak end of the continuum, suggesting the primacy of structure over motivation.

In many cases, the contact was someone only marginally included in the current network of contacts, such as an old college friend or a former workmate or employer, with whom sporadic contact had been maintained (Granovetter 1970, pp. 76-80). Usually such ties had not even been very strong when first forged. For work-related ties, respondents almost invariably said that they never saw the person in a nonwork context. Often when I asked respondents whether a friend had told them about their current job, they said, “Not a friend, an acquaintance.” It was the frequency of this comment which suggested this section of the paper to me. Chance meetings or mutual friends operated to reactivate such ties. It is remarkable that people receive crucial information from individuals whose very existence they have forgotten. Donald Light has suggested to me an alternative reason to expect predominance of weak ties in transfer of job information. He reasons that most of any given person’s ties are weak, so that we should expect, on a “random” model, that most ties through which job information flows should be weak. Since baseline data on acquaintance networks are lacking, this objection remains inconclusive. Even if the premise were correct, however, one might still expect that greater motivation of close friends would overcome their being outnumbered. Different assumptions yield different “random” models; it is not clear which one should be accepted as a starting point. One plausible such model would expect information to flow through ties in proportion to the time expended in interaction; this model would predict much more information via strong ties than one which merely counted all ties equally.

I also asked respondents where their contacts got the information they transmitted. In most cases, I traced the information to its initial source. I had expected that, as in the diffusion of rumors or diseases, long paths would be involved. But in 39.1% of the cases information came directly from the prospective employer, whom the respondent already knew; 45.3% said that there was one intermediary between himself and the employer; 12.5% reported two; and 3.1% more than two (N = 64). This suggests that for some important purposes it may be sufficient to discuss, as I have, the egocentric network made up of ego, his contacts, and their contacts. Had long information paths been involved, large numbers might have found out about any given job, and no particular tie would have been crucial. Such a model of job-information flow actually does correspond to the economists’ model of a “perfect” labor market. But those few who did acquire information through paths with more than one intermediary tended to be young and under the threat of unemployment; influence was much less likely to have been exerted by their contact on their behalf. These respondents were, in fact, more similar to those using formal intermediaries (agencies, advertisements) than to those hearing through short paths: both of the former are badly placed and dissatisfied in the labor market, and both receive information without influence. Just as reading about a job in the newspaper affords one no recommendation in applying for it, neither does it to have heard about it fifth hand.

The usual dichotomy between “formal” or mass procedures and diffusion through personal contacts may thus be invalid in some cases where, instead, the former may be seen as a limiting case of long diffusion chains. This is especially likely where information of instrumental significance is involved. Such information is most valuable when earmarked for one person.

From the individual’s point of view, then, weak ties are an important resource in making possible mobility opportunity. Seen from a more macroscopic vantage, weak ties play a role in effecting social cohesion. When a man changes jobs, he is not only moving from one network of ties to another, but also establishing a link between these. Such a link is often of the same kind which facilitated his own movement. Especially within professional and technical specialties which are well defined and limited in size, this mobility sets up elaborate structures of bridging weak ties between the more coherent clusters that constitute operative networks in particular locations. Information and ideas thus flow more easily through the specialty, giving it some “sense of community,” activated at meetings and conventions. Maintenance of weak ties may well be the most important consequence of such meetings.

Weak Ties and Community Organization

These comments about sense of community may remind us that in many cases it is desirable to deal with a unit of analysis larger than a single individual. I would like to develop my argument further by analyzing, in this section, why some communities organize for common goals easily and effectively whereas others seem unable to mobilize resources, even against dire threats. The Italian community of Boston’s West End, for example, was unable to even form an organization to fight against the “urban renewal” which ultimately destroyed it. This seems especially anomalous in view of Gans’s description of West End social structure as cohesive (1962).

Variations in culture and personality are often cited to explain such anomalies. Gans contrasts “lower”-, “working”-, and “middle”-class subcultures, concluding that only the last provides sufficient trust in leaders and practice in working toward common goals to enable formation of an effective organization. Thus, the working-class West End could not resist urban renewal (pp. 229-304). Yet, numerous well-documented cases show that some working-class communities have mobilized quite successfully against comparable or lesser threats (Dahl 1961, pp. 192-99; Keyes 1969; Davies 1966, chap. 4). This point was brought to my attention by Richard Wolfe. I would suggest, as a sharper analytical tool, examination of the network of ties comprising a community to see whether aspects of its structure might facilitate or block organization.

Imagine, to begin with, a community completely partitioned into cliques, such that each person is tied to every other in his clique and to none outside. Community organization would be severely inhibited. Leafletting, radio announcements, or other methods could insure that everyone was aware of some nascent organization; but studies of diffusion and mass communication have shown that people rarely act on mass-media information unless it is also transmitted through personal ties (Katz and Lazarsfeld 1955; Rogers 1962); otherwise one has no particular reason to think that an advertised product or an organization should be taken seriously. Enthusiasm for an organization in one clique, then, would not spread to others but would have to develop independently in each one to insure success.

The problem of trust is closely related. I would propose that whether a person trusts a given leader depends heavily on whether there exist intermediary personal contacts who can, from their own knowledge, assure him that the leader is trustworthy, and who can, if necessary, intercede with the leader or his lieutenants on his behalf. Trust in leaders is integrally related to the capacity to predict and affect their behavior. Leaders, for their part, have little motivation to be responsive or even trustworthy toward those to whom they have no direct or indirect connection. Thus, network fragmentation, by reducing drastically the number of paths from any leader to his potential followers, would inhibit trust in such leaders. This inhibition, furthermore, would not be entirely irrational.

Could the West End’s social structure really have been of this kind? Note first that while the structure hypothesized is, by definition, extremely fragmented, this is evident only at a macroscopic level—from an “aerial view” of the network. The local phenomenon is cohesion. (Davis [1967] also noted this paradox, in a related context.) An analyst studying such a group by participant observation might never see the extent of fragmentation, especially if the cliques were not earmarked by ethnic, cultural, or other visible differences. In the nature of participant observation, one is likely to get caught up in a fairly restricted circle; a few useful contacts are acquired and relied on for introduction to others. The “problem of entry into West End society was particularly vexing,” Gans writes. But eventually, he and his wife “were welcomed by one of our neighbors and became friends with them. As a result they invited us to many of their evening gatherings and introduced us to other neighbors, relatives and friends. … As time went on… other West Enders . . . introduced me to relatives and friends, although most of the social gatherings at which I participated were those of our first contact and their circle” (1962, pp. 340-41; emphasis supplied). Thus, his account of cohesive groups is not inconsistent with overall fragmentation.

Now, suppose that all ties in the West End were either strong or absent, and that the triad of figure 1 did not occur. Then, for any ego, all his friends were friends of one another, and all their friends were ego’s friends as well. Unless each person was strongly tied to all others in the community, network structure did indeed break down into the isolated cliques posited above. (In terms of Davis’s mathematical treatment, the overall network was ‘‘clusterable,”’ with unique clusters [1967, p. 186].) Since it is unlikely that anyone could sustain more than a few dozen strong ties, this would, in fact, have been the result.

Did strong ties take up enough of the West Enders’ social time to make this analysis even approximately applicable? Gans reported that “sociability is a routinized gathering of a relatively unchanging peer group of family members and friends that takes place several times a week.” Some “participate in informal cliques and in clubs made up of unrelated people… . In number, and in the amount of time devoted to them, however, these groups are much less important than the family circle” (1962, pp. 74, 80). Moreover, two common sources of weak ties, formal organizations and work settings, did not provide them for the West End; organization membership was almost nil (pp. 104-7) and few worked within the area itself, so that ties formed at work were not relevant to the community (p. 122).

Nevertheless, in a community marked by geographic immobility and lifelong friendships (p. 19) it strains credulity to suppose that each person would not have known a great many others, so that there would have been some weak ties. The question is whether such ties were bridges. See Jane Jacobs’s excellent, intuitive, discussion of bridging ties (“hop-skip links’’) in community organization (1961, chap. 6.) If none were, then the community would be fragmented in exactly the same way as described above, except that the cliques would then contain weak as well as strong ties. (This follows, again, from Davis’s analysis of “clusterability,” with strong and weak ties called ‘positive’ and absent ones “negative” [1967].) Such a pattern is made plausible by the lack of ways in the West End to develop weak ties other than by meeting friends of friends (where “friend” includes relatives)—in which case the new tie is automatically not a bridge. It is suggested, then, that for a community to have many weak ties which bridge, there must be several distinct ways or contexts in which people may form them. The case of Charlestown, a working-class community which successfully organized against the urban renewal plan of the same city (Boston) against which the West End was powerless, is instructive in this respect: unlike the West End, it had a rich organizational life, and most male residents worked within the area (Keyes 1969, chap. 4).

In the absence of actual network data, all this is speculation. The hard information needed to show either that the West End was fragmented or that communities which organized successfully were not, and that both patterns were due to the strategic role of weak ties, is not at hand and would not have been simple to collect. Nor has comparable information been collected in any context. But a theoretical framework has, at least, been suggested, with which one could not only carry out analyses post hoc, but also predict differential capacity of communities to act toward common goals. A rough principle with which to begin such an investigation might be: the more local bridges (per person?) in a community and the greater their degree, the more cohesive the community and the more capable of acting in concert. Study of the origins and nature (strength and content, for example) of such bridging ties would then offer unusual insight into the social dynamics of the community.

Micro and Macro Network Models

Unlike most models of interpersonal networks, the one presented here is not meant primarily for application to small, face-to-face groups or to groups in confined institutional or organizational settings. Rather, it is meant for linkage of such small-scale levels with one another and with larger, more amorphous ones. This is why emphasis here has been placed more on weak ties than on strong. Weak ties are more likely to link members of different small groups than are strong ones, which tend to be concentrated within particular groups.

For this reason, my discussion does not lend itself to elucidation of the internal structure of small groups. This point can be made more clearly by contrasting the model of this paper to one with which it shares many similarities, that of James Davis, Paul Holland, and Samuel Leinhardt (hereafter, the DHL model) (Davis 1970; Davis and Leinhardt 1971; Holland and Leinhardt 1970, 1971a, 19715; Davis, Holland, and Leinhardt 1971; Leinhardt 1972). The authors, inspired by certain propositions in George Homans’s The Human Group (1950), argue that “the central proposition in structural sociometry is this: Interpersonal choices tend to be transitive—if P chooses O and O chooses X, then P is likely to choose X” (Davis et al. 1971, p. 309). When this is true without exception, a sociogram can be divided into cliques in which every individual chooses every other; any asymmetric choices or nonchoices are between such cliques, and asymmetry, if present, runs only in one direction. A partial ordering of cliques may thus be inferred. If mutual choice implies equal, and assymmetric choice unequal, status, then this ordering reflects the stratification structure of the group (Holland and Leinhardt 1971a, pp. 107-14).

One immediate difference between this model and mine is that it is cast in terms of “choices” rather than ties. Most sociometric tests ask people whom they like best or would prefer to do something with, rather than with whom they actually spend time. If transitivity is built more into our cognitive than our social structure, this method might overstate its prevalence. But since the DHL model could recast in terms of ties, this is not a conclusive difference.

More significant is the difference in the application of my argument to transitivity. Let P choose O and O choose X (or equivalently, let X choose O and O choose P): then I assert that transitivity—P choosing X (or X, P)—is most likely when both ties—P-O and O-X—are strong, least likely when both are weak, and of intermediate probability if one is strong and one weak. Transitivity, then, is claimed to be a function of the strength of ties, rather than a general feature of social structure.

The justification of this assertion is, in part, identical with that offered earlier for the triad designated A-B-C. In addition, it is important to point out here that the DHL model was designed for small groups, and with increasing size of the group considered the rationale for transitivity weakens. If P chooses O and O chooses X, P should choose X out of consistency; but if P does not know or barely knows X, nonchoice implies no inconsistency. For the logic of transitivity to apply, a group must be small enough so that any person knows enough about every other person to be able to decide whether to “choose” him, and encounters him often enough that he feels the need for such a decision. Including weak ties in my model, then, lessens the expectation of transitivity and permits analysis of inter-group relationships and also of amorphous chunks of social structure which an analyst may ferret out as being of interest, but which are not easily defined in terms of face-to-face groups. Anthropologists have recently referred to such chunks as “quasi-groups” (Mayer 1966; Boissevain 1968).

Since, as I have argued above, weak ties are poorly represented in sociograms, there is little in the DHL empirical studies—which apply statistical tests to sociometric data—to confirm or disconfirm my argument on transitivity. One finding does lend itself to speculation, however. Leinhardt (1972) shows that the sociograms of schoolchildren conform more and more closely to the transitive model as they become older, sixth graders being the oldest tested. He interprets this as reflecting cognitive development—increasing capacity to make use of transitive logic. If my assertion is correct, an alternative possibility would be that children develop stronger ties with increasing age. This is consistent with some theories of child development (see especially Sullivan 1953, chap. 16) and would imply, on my argument, greater transitivity of structure. Some support for this explanation comes from Leinhardt’s finding that proportion of choices which were mutual was positively correlated with both grade level and degree of transitivity. In these sociograms, with an average of only about four choices per child, it seems likely that most mutual choices reflected strong ties (see n. 7, above).

Conclusion

The major implication intended by this paper is that the personal experience of individuals is closely bound up with larger-scale aspects of social structure, well beyond the purview or control of particular individuals. Linkage of micro and macro levels is thus no luxury but of central importance to the development of sociological theory. Such linkage generates paradoxes: weak ties, often denounced as generative of alienation (Wirth 1938) are here seen as indispensable to individuals’ opportunities and to their integration into communities; strong ties, breeding local cohesion, lead to overall fragmentation. Paradoxes are a welcome antidote to theories which explain everything all too neatly.

The model offered here is a very limited step in the linking of levels; it is a fragment of a theory. Treating only the strength of ties ignores, for instance, all the important issues involving their content. What is the relation between strength and degree of specialization of ties, or between strength and hierarchical structure? How can “negative” ties be handled? Should tie strength be developed as a continuous variable? What is the developmental sequence of network structure over time?

As such questions are resolved, others will arise. Demography, coalition structure, and mobility are just a few of the variables which would be of special importance in developing micro-macro linkage with the help of network analysis; how these are related to the present discussion needs specification. My contribution here is mainly, then, exploratory and programmatic, its primary purpose being to generate interest in the proposed program of theory and research.