What is Life? The Physical Aspect of the Living Cell
This short book, written by Schrodinger, one of the fathers of quantum mechanics, influenced the discovery of DNA. In 1943, in this book, he predicted the presence of ‘an aperiodic crystal’ and how it is a ‘code-script’ for how organisms work. Within 10 years, in 1953, DNA was discovered and it is both aperiodic and code-script of life! He also shows how life is unintuitive according to known physical laws, how it feeds on ‘negative entropy’ and how we need different type of laws to explain life. Epilogue On Determinism and Free Will is a cherry on the top and gives a physicist view on the topic. Written for dilettantes like myself (Schrodinger himself being one), this book is highly readable and relevant.
Yellow highlights/annotations are my own. You can disable them.Based on lectures delivered under the auspices of the Dublin Institute for Advanced Studies at Trinity College, Dublin, in February 1943. To the memory of My Parents
Preface
A scientist is supposed to have a complete and thorough I of knowledge, at first hand, of some subjects and, therefore, is usually expected not to write on any topic of which he is not a life, master. This is regarded as a matter of noblesse oblige. For the present purpose I beg to renounce the noblesse, if any, and to be the freed of the ensuing obligation. My excuse is as follows: We have inherited from our forefathers the keen longing for unified, all-embracing knowledge. The very name given to the highest institutions of learning reminds us, that from antiquity to and throughout many centuries the universal aspect has been the only one to be given full credit. But the spread, both in and width and depth, of the multifarious branches of knowledge by during the last hundred odd years has confronted us with a queer dilemma. We feel clearly that we are only now beginning to acquire reliable material for welding together the sum total of all that is known into a whole; but, on the other hand, it has become next to impossible for a single mind fully to command more than a small specialized portion of it. I can see no other escape from this dilemma (lest our true who aim be lost for ever) than that some of us should venture to embark on a synthesis of facts and theories, albeit with second-hand and incomplete knowledge of some of them – and at the risk of making fools of ourselves. So much for my apology. The difficulties of language are not negligible. One’s native speech is a closely fitting garment, and one never feels quite at ease when it is not immediately available and has to be replaced by another. My thanks are due to Dr Inkster (Trinity College, Dublin), to Dr Padraig Browne (St Patrick’s College, Maynooth) and, last but not least, to Mr S. C. Roberts. They were put to great trouble to fit the new garment on me and to even greater trouble by my occasional reluctance to give up some ‘original’ fashion of my own. Should some of it have survived the mitigating tendency of my friends, it is to be put at my door, not at theirs. The head-lines of the numerous sections were originally intended to be marginal summaries, and the text of every chapter should be read in continuo.
E.S.
Dublin
September 1944
Homo liber nulla de re minus quam de morte cogitat; et ejus sapientia non mortis sed vitae meditatio est. SPINOZA’S Ethics, Pt IV, Prop. 67
(There is nothing over which a free man ponders less than death; his wisdom is, to meditate not on death but on life.)
Chapter 1: The Classical Physicist’s Approach to the Subject
This little book arose from a course of public lectures, delivered by a theoretical physicist to an audience of about four hundred which did not substantially dwindle, though warned at the outset that the subject-matter was a difficult one and that the lectures could not be termed popular, even though the physicist’s most dreaded weapon, mathematical deduction, would hardly be utilized. The reason for this was not that the subject was simple enough to be explained without mathematics, but rather that it was much too involved to be fully accessible to mathematics. Another feature which at least induced a semblance of popularity was the lecturer’s intention to make clear the fundamental idea, which hovers between biology and physics, to both the physicist and the biologist.
For actually, in spite of the variety of topics involved, the whole enterprise is intended to convey one idea only – one small comment on a large and important question. In order not to lose our way, it may be useful to outline the plan very briefly in advance. The large and important and very much discussed question is: How can the events in space and time which take place within the spatial boundary of a living organism be accounted for by physics and chemistry? The preliminary answer which this little book will endeavor to expound and establish can be summarized as follows: The obvious inability of present-day physics and chemistry to account for such events is no reason at all for doubting that they can be accounted for by those sciences.
Statistical Physics. The Fundamental Difference in Structure
That would be a very trivial remark if it were meant only to stimulate the hope of achieving in the future what has not been achieved in the past. But the meaning is very much more positive, viz. that the inability, up to the present moment, is amply accounted for. Today, thanks to the ingenious work of biologists, mainly of geneticists, during the last thirty or forty years, enough is known about the actual material structure of organisms and about their functioning to state that, and to tell precisely why present-day physics and chemistry could not possibly account for what happens in space and time within a living organism.
The arrangements of the atoms in the most vital parts of an organism and the interplay of these arrangements differ in a fundamental way from all those arrangements of atoms which physicists and chemists have hitherto made the object of their experimental and theoretical research. Yet the difference which I have just termed fundamental is of such a kind that it might easily appear slight to anyone except a physicist who is thoroughly imbued with the knowledge that the laws of physics and chemistry are statistical throughout. For it is in relation to the statistical point of view that the structure of the vital parts of living organisms differs so entirely from that of any piece of matter that we physicists and chemists have ever handled physically in our laboratories or mentally at our writing desks. It is well-nigh unthinkable that the laws and regularities thus discovered should happen to apply immediately to the behaviour of systems which do not exhibit the structure on which those laws and regularities are based.
The non-physicist cannot be expected even to grasp let alone to appreciate the relevance of the difference in ‘statistical structure’ stated in terms so abstract as I have just used. To give the statement life and colour, let me anticipate what will be explained in much more detail later, namely, that the most essential part of a living cell – the chromosome fibre may suitably be called an aperiodic crystal. In physics we have dealt hitherto only with periodic crystals. To a humble physicist’s mind, these are very interesting and complicated objects; they constitute one of the most fascinating and complex material structures by which inanimate nature puzzles his wits. Yet, compared with the aperiodic crystal, they are rather plain and dull. The difference in structure is of the same kind as that between an ordinary wallpaper in which the same pattern is repeated again and again in regular periodicity and a masterpiece of embroidery, say a Raphael tapestry, which shows no dull repetition, but an elaborate, coherent, meaningful design traced by the great master.
In calling the periodic crystal one of the most complex objects of his research, I had in mind the physicist proper. Organic chemistry, indeed, in investigating more and more complicated molecules, has come very much nearer to that ‘aperiodic crystal’ which, in my opinion, is the material carrier of life. And therefore it is small wonder that the organic chemist has already made large and important contributions to the problem of life, whereas the physicist has made next to none.
The Naive Physicist’s Approach to the Subject
After having thus indicated very briefly the general idea – or rather the ultimate scope – of our investigation, let me describe the line of attack.
I propose to develop first what you might call ‘a naive physicist’s ideas about organisms, that is, the ideas which might arise in the mind of a physicist who, after having learnt his physics and, more especially, the statistical foundation of his science, begins to think about organisms and about the way they behave and function and who comes to ask himself conscientiously whether he, from what he has learnt, from the point of view of his comparatively simple and clear and humble science, can make any relevant contributions to the question. It will turn out that he can.
The next step must be to compare his theoretical anticipations with the biological facts. It will then turn out that – though on the whole his ideas seem quite sensible – they need to be appreciably amended. In this way we shall gradually approach the correct view – or, to put it more modestly, the one that I propose as the correct one. Even if I should be right in this, I do not know whether my way of approach is really the best and simplest. But, in short, it was mine. The ‘naive physicist’ was myself. And I could not find any better or clearer way towards the goal than my own crooked one.
Why are the Atoms so Small?
A good method of developing ‘the naive physicist’s ideas’ is to start from the odd, almost ludicrous, question: Why are atoms so small? To begin with, they are very small indeed. Every little piece of matter handled in everyday life contains an enormous number of them. Many examples have been devised to bring this fact home to an audience, none of them more impressive than the one used by Lord Kelvin:
Suppose that you could mark the molecules in a glass of water; then pour the contents of the glass into the ocean and stir the latter thoroughly so as to distribute the marked molecules uniformly throughout the seven seas; if then you took a glass of water anywhere out of the ocean, you would find in it about a hundred of your marked molecules. The actual sizes of atoms lie between about 1/5000 and 1/2000 the wave-length of yellow light. The comparison is significant, because the wave-length roughly indicates the dimensions of the smallest grain still recognizable in the microscope. Thus it will be seen that such a grain still contains thousands of millions of atoms.
Now, why are atoms so small? Clearly, the question is an evasion. For it is not really aimed at the size of the atoms. It is concerned with the size of organisms, more particularly with the size of our own corporeal selves. Indeed, the atom is small, when referred to our civic unit of length, say the yard or the metre. In atomic physics one is accustomed to use the so-called Angstrom (abbr. A), which is the 1010th part of a metre, or in decimal notation 0.0000000001 metre. Atomic diameters range between 1 and 2A. Now those civic units (in relation to which the atoms are so small) are closely related to the size of our bodies. There is a story tracing the yard back to the humour of an English king whom his councillors asked what unit to adopt – and he stretched out his arm sideways and said: ‘Take the distance from the middle of my chest to my fingertips, that will do all right.’ True or not, the story is significant for our purpose. The king would naturally indicate a length comparable with that of his own body, knowing that anything else would be very inconvenient. With all his predilection for the Angstrom unit, the physicist prefers to be told that his new suit will require six and a half yards of tweed – rather than sixty-five thousand millions of Angstroms of tweed.
It thus being settled that our question really aims at the ratio of two lengths – that of our body and that of the atom – with an incontestable priority of independent existence on the side of the atom, the question truly reads: Why must our bodies be so large compared with the atom? I can imagine that many a keen student of physics or chemistry may have deplored the fact that everyone of our sense organs, forming a more or less substantial part of our body and hence (in view of the magnitude of the said ratio) being itself composed of innumerable atoms, is much too coarse to be affected by the impact of a single atom. We cannot see or feel or hear the single atoms. Our hypotheses with regard to them differ widely from the immediate findings of our gross sense organs and cannot be put to the test of direct inspection. Must that be so? Is there an intrinsic reason for it? Can we trace back this state of affairs to some kind of first principle, in order to ascertain and to understand why nothing else is compatible with the very laws of Nature? Now this, for once, is a problem which the physicist is able to clear up completely. The answer to all the queries is in the affirmative.
The Working of an Organism Requires Exact Physical Laws
If it were not so, if we were organisms so sensitive that a single atom, or even a few atoms, could make a perceptible impression on our senses – Heavens, what would life be like! To stress one point: an organism of that kind would most certainly not be capable of developing the kind of orderly thought which, after passing through a long sequence of earlier stages, ultimately results in forming, among many other ideas, the idea of an atom.
Even though we select this one point, the following considerations would essentially apply also to the functioning of organs other than the brain and the sensorial system. Nevertheless, the one and only thing of paramount interest to us in ourselves is, that we feel and think and perceive. To the physiological process which is responsible for thought and sense all the others play an auxiliary part, at least from the human point of view, if not from that of purely objective biology. Moreover, it will greatly facilitate our task to choose for investigation the process which is closely accompanied by subjective events, even though we are ignorant of the true nature of this close parallelism. Indeed, in my view, it lies outside the range of natural science and very probably of human understanding altogether.
We are thus faced with the following question: Why should an organ like our brain, with the sensorial system attached to it, of necessity consist of an enormous number of atoms, in order that its physically changing state should be in close and intimate correspondence with a highly developed thought? On what grounds is the latter task of the said organ incompatible with being, as a whole or in some of its peripheral parts which interact directly with the environment, a mechanism sufficiently refined and sensitive to respond to and register the impact of a single atom from outside?
The reason for this is, that what we call thought (1) is itself an orderly thing, and (2) can only be applied to material, i.e. to perceptions or experiences, which have a certain degree of orderliness. This has two consequences. First, a physical organization, to be in close correspondence with thought (as my brain is with my thought) must be a very well-ordered organization, and that means that the events that happen within it must obey strict physical laws, at least to a very high degree of accuracy. Secondly, the physical impressions made upon that physically well-organized system by other bodies from outside, obviously correspond to the perception and experience of the corresponding thought, forming its material, as I have called it. Therefore, the physical interactions between our system and others must, as a rule, themselves possess a certain degree of physical orderliness, that is to say, they too must obey strict physical laws to a certain degree of accuracy.
Physical Laws Rest on Atomic Statistics and are Therefore Only Approximate
And why could all this not be fulfilled in the case of an organism composed of a moderate number of atoms only and sensitive already to the impact of one or a few atoms only?
Because we know all atoms to perform all the time a completely disorderly heat motion, which, so to speak, opposes itself to their orderly behaviour and does not allow the events that happen between a small number of atoms to enrol themselves according to any recognizable laws. Only in the co-operation of an enormously large number of atoms do statistical laws begin to operate and control the behaviour of these assemblies with an accuracy increasing as the number of atoms involved increases. It is in that way that the events acquire truly orderly features. All the physical and chemical laws that are known to play an important part in the life of organisms are of this statistical kind; any other kind of lawfulness and orderliness that one might think of is being perpetually disturbed and made inoperative by the unceasing heat motion of the atoms.
Their Precision is Based on the Large of Number of Atoms Intervening
First Example (Paramagnetism)
Let me try to illustrate this by a few examples, picked somewhat at random out of thousands, and possibly not just the best ones to appeal to a reader who is learning for the first time about this condition of things – a condition which in modern physics and chemistry is as fundamental as, say, the fact that organisms are composed of cells is in biology, or as Newton’s Law in astronomy, or even as the series of integers, 1, 2, 3, 4, 5, … in mathematics. An entire newcomer should not expect to obtain from the following few pages a full understanding and appreciation of the subject, which is associated with the illustrious names of Ludwig Boltzmann and Willard Gibbs and treated in textbooks under the name of ‘statistical thermodynamics’.
Figure 1: Paramagnetism
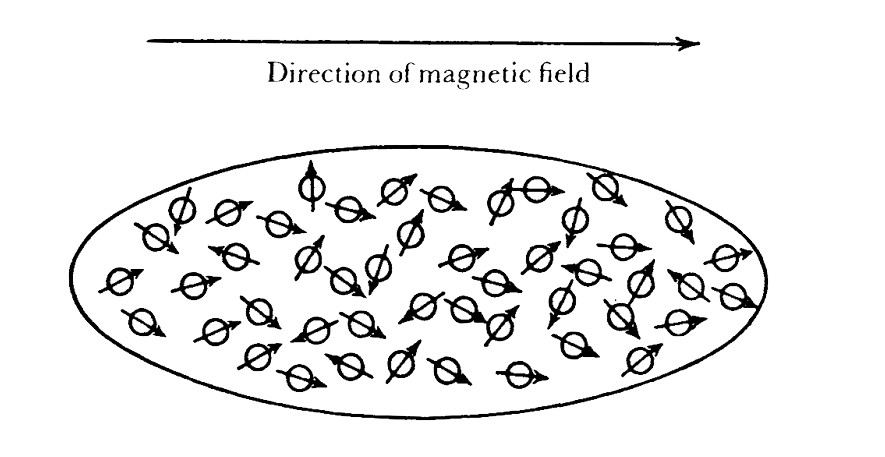
If you fill an oblong quartz tube with oxygen gas and put it into a magnetic field, you find that the gas is magnetized. The magnetization is due to the fact that the oxygen molecules are little magnets and tend to orientate themselves parallel to the field, like a compass needle. But you must not think that they actually all turn parallel. For if you double the field, you get double the magnetization in your oxygen body, and that proportionality goes on to extremely high field strengths, the magnetization increasing at the rate of the field you apply. This is a particularly clear example of a purely statistical law. The orientation the field tends to produce is continually counteracted by the heat motion, which works for random orientation. The effect of this striving is, actually, only a small preference for acute over obtuse angles between the dipole axes and the field. Though the single atoms change their orientation incessantly, they produce on the average (owing to their enormous number) a constant small preponderance of orientation in the direction of the field and proportional to it. This ingenious explanation is due to the French physicist P. Langevin. It can be checked in the following way.
If the observed weak magnetization is really the outcome of rival tendencies, namely, the magnetic field, which aims at combing all the molecules parallel, and the heat motion, which makes for random orientation, then it ought to be possible to increase the magnetization by weakening the heat motion, that is to say, by lowering the temperature, instead of reinforcing the field. That is confirmed by experiment, which gives the magnetization inversely proportional to the absolute temperature, in quantitative agreement with theory (Curie’s law). Modern equipment even enables us, by lowering the temperature, to reduce the heat motion to such insignificance that the orientating tendency of the magnetic field can assert itself, if not completely, at least sufficiently to produce a substantial fraction of ‘complete magnetization’. In this case we no longer expect that double the field strength will double the magnetization, but that the latter will increase less and less with increasing field, approaching what is called ‘saturation’. This expectation too is quantitatively confirmed by experiment. Notice that this behaviour entirely depends on the large numbers of molecules which co-operate in producing the observable magnetization. Otherwise, the latter would not be an constant at all, but would, by fluctuating quite irregularly of from one second to the next, bear witness to the vicissitudes of the contest between heat motion and field.
Second Example (Brownian Movement, Diffusion)
If you fill the lower part of a closed glass vessel with fog, pt consisting of minute droplets, you will find that the upper or boundary of the fog gradually sinks, with a well-defined velocity, determined by the viscosity of the air and the size and the specific gravity of the droplets. But if you look at one of the droplets under the microscope you find that it does not permanently sink with constant velocity, but performs a very irregular movement, the so-called Brownian movement, which corresponds to a regular sinking only on the average. Now these droplets are not atoms, but they are sufficiently small and light to be not entirely insusceptible to the impact of one single molecule of those which hammer their surface in perpetual impacts. They are thus knocked about and can only on the average follow the influence of gravity.
Figure 2 (left): Sinking Fog. Figure 3 (right): Brownian movement of a sinking droplet

This example shows what funny and disorderly experience we should have if our senses were susceptible to the impact of a few molecules only. There are bacteria and other organisms so small that they are strongly affected by this phenomenon. Their movements are determined by the thermic whims of the surrounding medium; they have no choice. If they had some locomotion of their own they might nevertheless succeed in on getting from one place to another -but with some difficulty, since the heat motion tosses them like a small boat in a rough sea.
Figure 4: Diffusion from left to right in a solution of varying concentration.

A phenomenon very much akin to Brownian movement is that of diffusion. Imagine a vessel filled with a fluid, say water, with a small amount of some coloured substance dissolved in it, say potassium permanganate, not in uniform concentration, but rather as in Fig. 4, where the dots indicate the molecules of the dissolved substance (permanganate) and the concentration diminishes from left to right. If you leave this system alone a very slow process of ‘diffusion’ sets in, the at permanganate spreading in the direction from left to right, that is, from the places of higher concentration towards the places of lower concentration, until it is equally distributed of through the water.
The remarkable thing about this rather simple and apparently not particularly interesting process is that it is in no way due, as one might think, to any tendency or force driving the permanganate molecules away from the crowded region to the less crowded one, like the population of a country spreading to those parts where there is more elbow-room. Nothing of the sort happens with our permanganate molecules. Every one of them behaves quite independently of all the others, which it very seldom meets. Everyone of them, whether in a crowded region or in an empty one, suffers the same fate of being continually knocked about by the impacts of the water molecules and thereby gradually moving on in an unpredictable direction -sometimes towards the higher, sometimes towards the lower, concentrations, sometimes obliquely. The kind of motion it performs has often been compared with that of a blindfolded person on a large surface imbued with a certain desire of ‘walking’, but without any preference for any particular direction, and so changing his line continuously.
That this random walk of the permanganate molecules, the same for all of them, should yet produce a regular flow towards the smaller concentration and ultimately make for uniformity of distribution, is at first sight perplexing – but only at first sight. If you contemplate in Fig. 4 thin slices of approximately constant concentration, the permanganate molecules which in a given moment are contained in a particular slice will, by their random walk, it is true, be carried with equal probability to the right or to the left. But precisely in consequence of this, a plane separating two neighbouring slices will be crossed by more molecules coming from the left than in the opposite direction, simply because to the left there are more molecules engaged in random walk than there are to the right. And as long as that is so the balance will show up as a regular flow from left to right, until a uniform distribution is reached.
When these considerations are translated into mathematical language the exact law of diffusion is reached in the form of a partial differential equation $\partial \rho/\partial t = D \nabla^2 \rho$, which I shall not trouble the reader by explaining, though its meaning in ordinary language is again simple enough. The reason for mentioning the stern ‘mathematically exact’ law here, is to emphasize that its physical exactitude must nevertheless be challenged in every particular application. Being based on pure chance, its validity is only approximate. If it is, as a rule, a very good approximation, that is only due to the enormous number of molecules that co-operate in the phenomenon. The smaller their number, the larger the quite haphazard deviations we must expect – and they can be observed under favourable circumstances.
Third Example (Limits of Accuracy of Measuring)
The last example we shall give is closely akin to the second one, but has a particular interest. A light body, suspended by a long thin fibre in equilibrium orientation, is often used by physicists to measure weak forces which deflect it from that position of equilibrium, electric, magnetic or gravitational forces being applied so as to twist it around the vertical axis. (The light body must, of course, be chosen appropriately for the particular purpose.) The continued effort to improve the accuracy of this very commonly used device of a ‘torsional balance’, has encountered a curious limit, most interesting in itself. In choosing lighter and lighter bodies and thinner and longer fibres – to make the balance susceptible to weaker and weaker forces – the limit was reached when the suspended body became noticeably susceptible to the impacts of the heat motion of the surrounding molecules and began to perform an incessant, irregular ‘dance’ about its equilibrium position, much like the trembling of the droplet in the second example.
Though this behaviour sets no absolute limit to the accuracy of measurements obtained with the balance, it sets a practical one. The uncontrollable effect of the heat motion competes with the effect of the force to be measured and makes the single deflection observed insignificant. You have to multiply observations, in order to eliminate the effect of the Brownian movement of your instrument. This example is, I think, particularly illuminating in our present investigation. For our to the organs of sense, after all, are a kind of instrument. We can see in the how useless they would be if they became too sensitive.
The √n Rule
So much for examples, for the present. I will merely add that there is not one law of physics or chemistry, of those that are relevant within an organism or in its interactions with its environment, that I might not choose as an example. The detailed explanation might be more complicated, but the salient point would always be the same and thus the description would become monotonous. But I should like to add one very important quantitative statement concerning the degree of inaccuracy to be expected in any physical law, the so-called √n law. I will first illustrate it by a simple example and then generalize it.
If I tell you that a certain gas under certain conditions of pressure and temperature has a certain density, and if I expressed this by saying that within a certain volume (of a size relevant for some experiment) there are under these conditions just n molecules of the gas, then you might be sure that if you could test my statement in a particular moment of time, you would find it inaccurate, the departure being of the order of √n. Hence if the number n = 100, you would find a departure of about 10, thus relative error = 10%. But n = 1 million, you would be likely to find a departure of about 1,000, thus relative error = 1/10%. Now, roughly speaking, this statistical law is quite general. The laws of physics and physical chemistry are inaccurate within a probable relative error of the order of 1/ √n, where n is the number of molecules that co-operate to bring about that law – to produce its validity within such regions of space or time (or both) that matter, for some considerations or for some particular experiment.
You see from this again that an organism must have a comparatively gross structure in order to enjoy the benefit of fairly accurate laws, both for its internal life and for its interplay with the external world. For otherwise the number of co-operating particles would be too small, the ‘law’ too inaccurate. The particularly exigent demand is the square root. For though a million is a reasonably large number, an accuracy of Just 1in 1,000 is not overwhelmingly good, If a thing claims the dignity of being a ‘Law of Nature’.
Chapter 2: The Hereditary Mechanism
The Classical Physicist’s Expectation, Far from Being Trivial, is Wrong
Thus we have come to the conclusion that an organism and all the biologically relevant processes that it experiences must have an extremely ‘many-atomic’ structure and must be safeguarded against haphazard, ‘single-atomic’ events attaining too great importance. That, the ‘naive physicist’ tells us, is essential, so that the organism may, so to speak, have sufficiently accurate physical laws on which to draw for setting up its marvellously regular and well-ordered working. How do these conclusions, reached, biologically speaking, a priori (that is, from the purely physical point of view), fit in with actual biological facts?
At first sight one is inclined to think that the conclusions are little more than trivial. A biologist of, say, thirty years ago might have said that, although it was quite suitable for a popular lecturer to emphasize the importance, in the organism as elsewhere, of statistical physics, the point was, in fact, rather a familiar truism. For, naturally, not only the body of an adult individual of any higher species, but every single cell composing it contains a ‘cosmical’ number of single atoms of every kind. And every particular physiological process that we observe, either within the cell or in its interaction with the cell environment, appears – or appeared thirty years ago – to involve such enormous numbers of single atoms and single atomic processes that all the relevant laws of physics and physical chemistry would be safeguarded even under the very exacting demands of statistical physics in respect of large numbers; this demand illustrated just now by the √n rule.
Today, we know that this opinion would have been a mistake. As we shall presently see, incredibly small groups of atoms, much too small to display exact statistical laws, do play a dominating role in the very orderly and lawful events within a living organism. They have control of the observable large-scale features which the organism acquires in the course of its development, they determine important characteristics of its functioning; and in all this very sharp and very strict biological laws are displayed.
I must begin with giving a brief summary of the situation in biology, more especially in genetics – in other words, I have to summarize the present state of knowledge in a subject of which I am not a master. This cannot be helped and I apologize, particularly to any biologist, for the dilettante character of my summary. On the other hand, I beg leave to put the prevailing ideas before you more or less dogmatically. A poor theoretical physicist could not be expected to produce anything like a competent survey of the experimental evidence, which consists of a large number of long and beautifully interwoven series of breeding experiments of truly unprecedented ingenuity on the one hand and of direct observations of the living cell, conducted with all the refinement of modern microscopy, on the other.
The Hereditary Code-Script (Chromosomes)
Let me use the word ‘pattern’ of an organism in the sense in be which the biologist calls it ‘the four-dimensional pattern’, meaning not only the structure and functioning of that organism in the adult, or in any other particular stage, but the whole of its ontogenetic development from the fertilized egg the cell to the stage of maturity, when the organism begins to reproduce itself. Now, this whole four-dimensional pattern is known to be determined by the structure of that one cell, the fertilized egg. Moreover, we know that it is essentially determined by the structure of only a small part of that cell, its large nucleus. This nucleus, in the ordinary ‘resting state’ of the cell, usually appears as a network of chromatine, distributed over the cell. But in the vitally important processes of cell division (mitosis and meiosis, see below) it is seen to consist of a set of particles, usually fibre-shaped or rod-like, called the chromosomes, which number 8 or 12 or, in man, 48. But I ought really to have written these illustrative numbers as 2 X 4, 2 X 6, …, 2 X 24, …, and I ought to have spoken of two sets, in order to use the expression in the customary strict meaning of the biologist. For though the single chromosomes are sometimes clearly distinguished and individualized by shape and size, the two sets are almost entirely alike. As we have shall see in a moment, one set comes from the mother (egg cell), one from the father (fertilizing spermatozoon). It is these chromosomes, or probably only an axial skeleton fibre of what we actually see under the microscope as the chromosome, that contain in some kind of code-script the entire pattern of the individual’s future development and of its functioning in the mature state. Every complete set of chromosomes contains the full code; so there are, as a rule, two copies of the latter in the fertilized egg cell, which forms the earliest stage of the future individual.
In calling the structure of the chromosome fibres a code-script we mean that the all-penetrating mind, once conceived by Laplace, to which every causal connection lay immediately open, could tell from their structure whether the egg would develop, under suitable conditions, into a black cock or into a speckled hen, into a fly or a maize plant, a rhododendron, a beetle, a mouse or a woman. To which we may add, that the appearances of the egg cells are very often remarkably similar; and even when they are not, as in the case of the comparatively gigantic eggs of birds and reptiles, the difference is not been so much the relevant structures as in the nutritive material which in these cases is added for obvious reasons. But the term code-script is, of course, too narrow. The chromosome structures are at the same time instrumental in bringing about the development they foreshadow. They are law-code and executive power – or, to use another simile, they are architect’s plan and builder’s craft – in one.
Growth of the Body by Cell Division (Mitosis)
How do the chromosomes behave in ontogenesis? The growth of an organism is effected by consecutive cell divisions. Such a cell division is called mitosis. It is, in the life of a cell, not such a very frequent event as one might expect, considering the enormous number of cells of which our body is composed. In the beginning the growth is rapid. The egg divides into two ‘daughter cells’ which, at the next step, will produce a generation of four, then of 8, 16, 32, 64, …, etc. The frequency of division will not remain exactly the same in all parts of the growing body, and that will break the regularity of these numbers. But from their rapid increase we infer by an easy computation that on the average as few as 50 or 60 successive divisions suffice to produce the number of cells in a grown man – or, say, ten times the number, taking into account the exchange of cells during lifetime. Thus, a body cell of mine is, on the average, only the 50th or 60th ‘descendant’ of the egg that was I.
In Mitosis Every Chromosome is Duplicated
How do the chromosomes behave on mitosis? They duplicate – both sets, both copies of the code, duplicate. The process has been intensively studied under the microscope and is of paramount interest, but much too involved to describe here in detail. The salient point is that each of the two ‘daughter cells’ gets a dowry of two further complete sets of chromosomes exactly similar to those of the parent cell. So all the body cells are exactly alike as regards their chromosome treasure.
However little we understand the device we cannot but think that it must be in some way very relevant to the functioning of the organism, that every single cell, even a less important one, should be in possession of a complete (double) copy of the code-script. Some time ago we were told in the newspapers that in his African campaign General Montgomery made a point of having every single soldier of his army meticulously informed of all his designs. If that is true (as it conceivably might be, considering the high intelligence and reliability of his troops) it provides an excellent analogy to our case, in which the corresponding fact certainly is literally true. The most surprising fact is the doubleness of the chromosome set, maintained throughout the mitotic divisions. That it is the outstanding feature of the genetic mechanism is most strikingly revealed by the one and only departure from the rule, which we have now to discuss.
Reductive Division (Meiosis) and Fertilization (Syngamy)
Very soon after the development of the individual has set in, a group of cells is reserved for producing at a later stage the so-called gametes, the sperm cells or egg cells, as the case may be, needed for the reproduction of the individual in maturity. ‘Reserved’ means that they do not serve other purposes in the meantime and suffer many fewer mitotic divisions. The exceptional or reductive division (called meiosis) is the one by which eventually, on maturity, the gametes posed to are produced from these reserved cells, as a rule only a short time before syngamy is to take place. In meiosis the double chromosome set of the parent cell simply separates into two single sets, one of which goes to each of the two daughter cells, the gametes. In other words, the mitotic doubling of the number of chromosomes does not take place in meiosis, the number remains constant and thus every gamete receives only half – that is, only one complete copy of the code, not two, e.g. in man only 24, not 2 X 24 = 48.
Cells with only one chromosome set are called haploid (from Greek απλοπχ, single). Thus the gametes are haploid, the ordinary body cells diploid (from Greek Οπλπχ, double). Individuals with three, four, …or generally speaking with many chromosome sets in all their body cells occur occasionally; the latter are then called triploid, tetraploid, …, polyploid. In the act of syngamy the male gamete (spermatozoon) and the female gamete (egg), both haploid cells, coalesce to form the fertilized egg cell, which is thus diploid. One of its chromosome sets comes from the mother, one from the father.
Haploid Individuals
One other point needs rectification. Though not indispensable for our purpose it is of real interest, since it shows that actually a fairly complete code-script of the ‘pattern’ is contained in every single set of chromosomes.
There are instances of meiosis not being followed shortly after by fertilization, the haploid cell (the ‘gamete’) undergoing meanwhile numerous mitotic cell divisions, which result in building up a complete haploid individual. This is the case in the male bee, the drone, which is produced parthenogenetically, that is, from non-fertilized and therefore haploid eggs of the queen. The drone has no father! All its body cells are haploid. If you please, you may call it a grossly exaggerated spermatozoon; and actually, as everybody knows, to function as such happens to be its one and only task in life. However, that is perhaps a ludicrous point of view. For the case is not two quite unique. There are families of plants in which the haploid gamete which is produced by meiosis and is called a spore in the such cases falls to the ground and, like a seed, develops into a the true haploid plant comparable in size with the diploid.
Figure 5: Alternation of Generations.
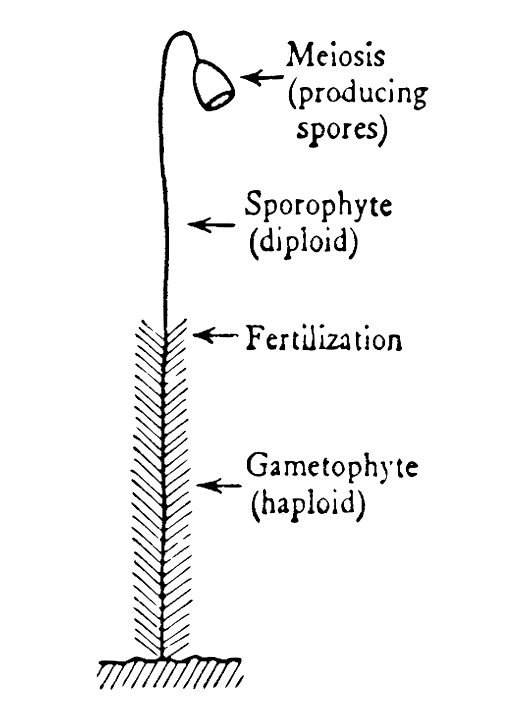
Fig. 5 is a rough sketch of a moss, well known in our forests. The leafy lower part is the haploid plant, called the gametophyte, because at its upper end it develops sex organs and gametes, which by mutual fertilization produce in the ordinary way the diploid plant, the bare stem with the capsule at the top. This is called the sporophyte, because it produces, by meiosis, the spores in the capsule at the top. When the capsule opens, the spores fall to the ground and develop into a leafy stem, etc. The course of events is appropriately called alternation of generations. You may, if you choose, look upon the ordinary case, man and the animals, in the same way. But the ‘gametophyte’ is then as a rule a very short-lived, unicellular generation, spermatozoon or egg cell as the case may be. Our body corresponds to the sporophyte. Our ‘spores’ are the reserved cells from which, by meiosis, the unicellular generation springs.
The Outstanding Relevance of the Reductive Division
The important, the really fateful event in the process of reproduction of the individual is not fertilization but meiosis. One set of chromosomes is from the father, one from the mother. Neither chance nor destiny can interfere with that. Every man owes just half of his inheritance to his mother, half of it to his father. That one or the other strain seems often to prevail is due to other reasons which we shall come to later. (Sex itself is, of course, the simplest instance of such prevalence.).
But when you trace the origin of your inheritance back to your grandparents, the case is different. Let me fix attention on my paternal set of chromosomes, in particular on one of them, say No. 5. It is a faithful replica either of the No. 5 my father received from his father or of the No. 5 he had received from his mother. The issue was decided by a 50:50 chance in the meiosis taking place in my father’s body in November 1886 and producing the spermatozoon which a few days later was to be effective in begetting me. Exactly the same story could be repeated about chromosomes Nos. 1, 2, 3, …, 24 of my paternal set, and mutatis mutandis about every one of my maternal chromosomes. Moreover, all the 48 issues are entirely independent. Even if it were known that my paternal chromosome No. 5 came from my grandfather Josef Schrodinger, the No.7 still stands an equal chance of being either also from him, or from his wife Marie, nee Bogner.
Crossing-Over. Location Of Properties
But pure chance has been given even a wider range in mixing the grandparental inheritance in the offspring than would appear from the preceding description, in which it has been tacitly assumed, or even explicitly stated, that a particular chromosome as a whole was either from the grandfather or back to from the grandmother; in other words that the single chromosomes are passed on undivided. In actual fact they are not, or not always. Before being separated in the reductive division, any two ‘homologous’ chromosomes come into close contact with each other, during chance in which they sometimes exchange entire portions in the way illustrated in Fig. 6. By this process, called ‘crossing-over’, two properties situated in the respective parts of that chromosome will be separated in the grandchild, who will follow the grandfather in one of them, the grandmother in the other one. The act of crossing-over, being neither very rare nor very issues are frequent, has provided us with invaluable information regarding the location of properties in the chromosomes. For a full account we should have to draw on conceptions not introduced before the next chapter (e.g. heterozygosy, dominance, etc.); but as that would take us beyond the range of this little book, let me indicate the salient point right away.
Figure 6: Crossing-over. Left: the two homologous chromosomes in contact. Right: after exchange and separation.
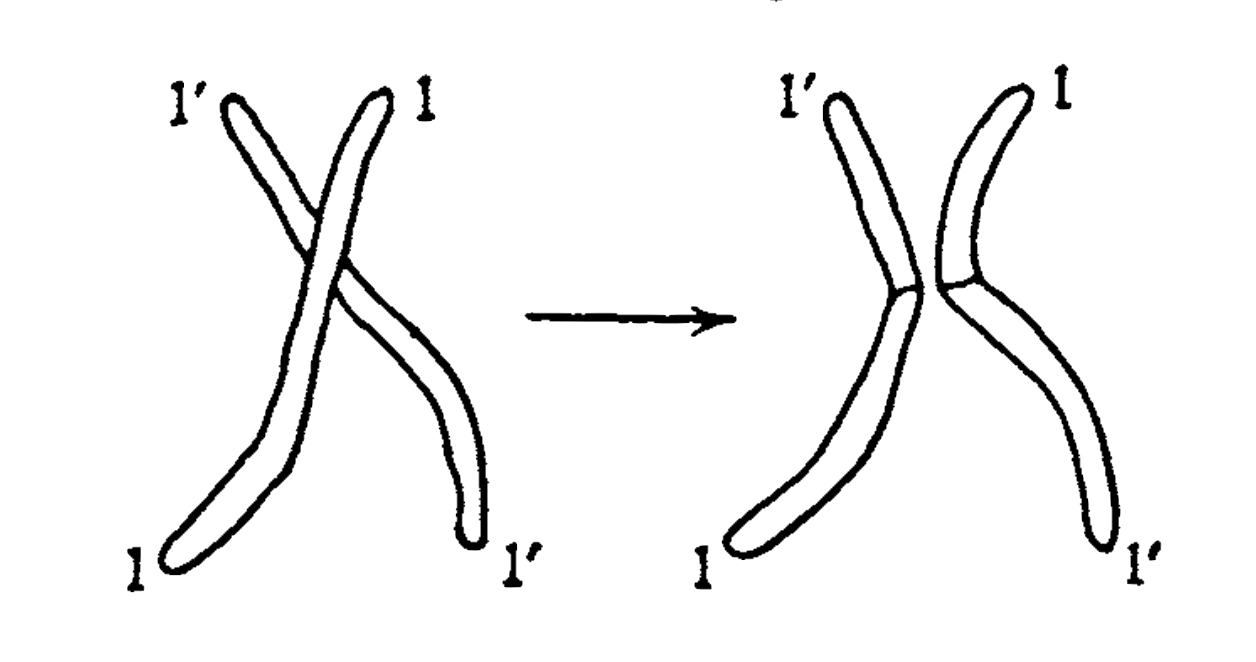
If there were no crossing-over, two properties for which the same chromosome is responsible would always be passed on in mixing together, no descendant receiving one of them without receiving the other as well; but two properties due to different chromosomes, would either stand a 50:50 chance of being separated or they would invariably be separated – the latter when they were situated in homologous chromosomes of the same ancestor, which could never go together.
These rules and chances are interfered with by crossing-over. Hence the probability of this event can be ascertained by registering carefully the percentage composition of the off-spring in extended breeding experiments, suitably laid out for at the purpose. In analysing the statistics, one accepts the suggestive working hypothesis that the ‘linkage’ between two properties situated in the same chromosome, is the less frequently broken by crossing-over, the nearer they lie to each other. For then there is less chance of the point of exchange lying between them, whereas properties located near the opposite ends of the chromosomes are separated by every crossing-over. (Much the same applies to the recombination of properties located in homologous chromosomes of the same ancestor.) In this way one may expect to get from the ‘statistics of linkage’ a sort of ‘map of properties’ within every chromosome.
These anticipations have been fully confirmed. In the cases to which tests have been thoroughly applied (mainly, but not only, Drosophila) the tested properties actually divide into as many separate groups, with no linkage from group to group, as there are different chromosomes (four in Drosophila). Within every group a linear map of properties can be drawn up which accounts quantitatively for the degree of linkage it between any two of that group, so that there is little doubt that they actually are located, and located along a line, as the rod-like shape of the chromosome suggests.
Of course, the scheme of the hereditary mechanism, as drawn up here, is still rather empty and colourless, even slightly naive. For we have not said what exactly we understand by a property. It seems neither adequate nor possible to dissect into discrete ‘properties’ the pattern of an organism which is essentially a unity, a ‘whole’. Now, what we actually state in any particular case is, that a pair of ancestors were different in a certain well-defined respect (say, one had blue eyes, the other brown), and that the offspring follows in this respect either one or the other. What we locate in the chromosome is the seat of this difference. (We call it, in technical language, a ‘locus’, or, if we think of the hypothetical material structure underlying it, a ‘gene’.) Difference of property, to my view, is really the fundamental concept rather than property itself, notwithstanding the apparent linguistic and logical contradiction of this statement. The differences of the properties actually are discrete, as will emerge in the next chapter when we have to speak of mutations and the dry scheme hitherto presented will, as I hope, acquire more life and colour.
Maximum Size of a Gene
We have just introduced the term gene for the hypothetical same material carrier of a definite hereditary feature. We must now the stress two points which will be highly relevant to our every investigation. The first is the size – or, better, the maximum size – of such a carrier; in other words, to how small a volume can we trace the location? The second point will be the permanence of a gene, to be inferred from the durability of the hereditary pattern.
As regards the size, there are two entirely independent estimates, one resting on genetic evidence (breeding experiments), the other on cytological evidence (direct microscopic inspection). The first is, in principle, simple enough. After having, in the way described above, located in the chromosome a considerable number of different (large-scale) features (say of the Drosophila fly) within a particular one of its chromosomes, to get the required estimate we need only divide the measured length of that chromosome by the number of features and multiply by the cross-section. For, of course, we count as different only such features as are occasionally separated by crossing-over, so that they cannot be due to the same (microscopic or molecular) structure. On the other hand, it is clear that our estimate can only give a maximum size, because the number of features isolated by in this genetic analysis is continually increasing as work goes on.
The other estimate, though based on microscopic inspection, is really far less direct. Certain cells of Drosophila (namely, those of its salivary glands) are, for some reason, enormously enlarged, and so are their chromosomes. In them you distinguish a crowded pattern of transverse dark bands across the fibre. C. D. Darlington has remarked that the number of these bands (2,000 in the case he uses) is, though, considerably larger, yet roughly of the same order of magnitude as the number of genes located in that chromosome by breeding experiments. He inclines to regard these bands as indicating the actual genes (or separations of genes). Dividing the length of the chromosome, measured in a normal-sized cell by their number (2,000) he finds the volume of a gene equal to a cube of edge 300 Å. Considering the roughness of the estimates, we may regard this to be also the size obtained by the first method.
Small Numbers
A full discussion of the bearing of statistical physics on all the facts I am recalling – or perhaps, I ought to say, of the bearing of these facts on the use of statistical physics in the living cell will follow later. But let me draw attention at this point to the fact that 300 Å is only about 100 or 150 atomic distances in a liquid or in a solid, so that a gene contains certainly not more than about a million or a few million atoms. That number is much too small (from the √n point of view) to entail an orderly and lawful behaviour according to statistical physics – and that means according to physics. It is too small, even if all these atoms played the same role, as they do in a gas or in a drop of liquid. And the gene is most certainly not just a homogeneous drop of liquid. It is probably a large protein molecule, in which every atom, every radical, every heterocyclic ring plays an individual role, more or less different from that played by any of the other similar atoms, radicals, or rings. This, at any rate, is the opinion of leading geneticists such as Haldane and Darlington, and we shall soon have to refer to genetic experiments which come very near to proving it.
Permanence
Let us now turn to the second highly relevant question: What degree of permanence do we encounter in hereditary properties and what must we therefore attribute to the material structures which carry them?
The answer to this can really be given without any special investigation. The mere fact that we speak of hereditary properties indicates that we recognize the permanence to be almost absolute. For we must not forget that what is passed on by the parent to the child is not just this or that peculiarity, a hooked nose, short fingers, a tendency to rheumatism, haemophilia, dichromasy, etc. Such features we may conveniently select for studying the laws of heredity. But actually it is the whole (four-dimensional) pattern of the ‘phenotype’, the all the visible and manifest nature of the individual, which is reproduced without appreciable change for generations, permanent within centuries – though not within tens of thousands of years – and borne at each transmission by the material structure of the nuclei of the two cells which unite to form the fertilized egg cell. That is a marvel – than which only one is greater; one that, if intimately connected with it, yet lies on a different plane. I mean the fact that we, whose total being is entirely based on a marvellous interplay of this very kind, yet possess the power of acquiring considerable knowledge about it. I think it possible that this knowledge may advance to little short of a complete understanding – of the first marvel. The second may well be beyond human understanding.
Chapter 3: Mutations
‘Jump-Like’ Mutations – The Working-Ground of Natural Selection
The general facts which we have just put forward in evidence of the durability claimed for the gene structure, are perhaps too familiar to us to be striking or to be regarded as convincing. Here, for once, the common saying that exceptions prove the rule is actually true. If there were no exceptions to the likeness between children and parents, we should have been deprived not only of all those beautiful experiments which have revealed to us the detailed mechanism of heredity, but also of that grand, million-fold experiment of Nature, which forges the species by natural selection and survival of the fittest.
Let me take this last important subject as the starting-point for presenting the relevant facts – again with an apology and a reminder that I am not a biologist: We know definitely, today, that Darwin was mistaken in regarding the small, continuous, accidental variations, that are bound to occur even in the most homogeneous population, as the material on which natural selection works. For it has been proved that they are not inherited.The fact is important enough to be illustrated briefly. If you take a crop of pure-strain barley, and measure, ear by ear, the length of its awns and plot the result of your statistics, you will get a bell-shaped curve as shown in Fig. 7, where the number of ears with a definite length of awn is plotted against the length. In other words: a definite medium length prevails, and deviations in either direction occur with certain frequencies. Now pick out a group of ears (as indicated by blackening) with awns noticeably beyond the average, but sufficient in number to be sown in a field by themselves and give a new crop. In making the same statistics for this, Darwin would have expected to find the corresponding curve shifted to the right. In other words, he would have expected to produce by selection an increase of the average length of the awns. That is not the case, if a truly pure-bred strain of barley has been used. The new statistical curve, obtained from the selected crop, is identical with the first one, and the same would be the case if ears with particularly short awns had been selected for seed.
Figure 7: Statistics of length of awns in a pure-bred crop. The black group is to be selected for sowing. (The details are not from an actual experiment, but are just set up for illustration.)
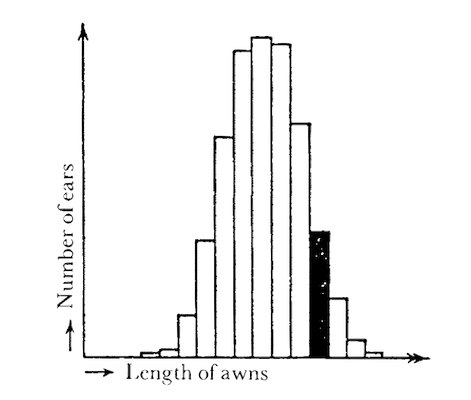
Selection has no effect – because the small, continuous variations are not inherited. They are obviously not based on the structure of the hereditary substance, they are accidental. But about forty years ago the Dutchman de Vries discovered that in the offspring even of thoroughly pure-bred stocks, a very small number of individuals, say two or three in tens of thousands, turn up with small but ‘jump-like’ changes, the expression ‘jump-like’ not meaning that the change is so very considerable, but that there is a discontinuity inasmuch as there are no intermediate forms between the unchanged and the few changed. De Vries called that a mutation. The significant fact is the discontinuity. It reminds a physicist of quantum theory – no intermediate energies occurring between two neighbouring energy levels. He would be inclined to call de Vries’s mutation theory, figuratively, the quantum theory of biology. We shall see later that this is much more than figurative. The mutations are actually due to quantum jumps in the gene molecule. But quantum theory was but two years old when de Vries first published his discovery, in 1902. Small wonder that it took another generation to discover the intimate connection!
They Breed True, That is, They are Perfectly Inherited
Mutations are inherited as perfectly as the original, unchanged characters were. To give an example, in the first crop of barley considered above a few ears might turn up with awns considerably outside the range of variability shown in Fig. 7, say with no awns at all. They might represent a de Vries mutation and would then breed perfectly true, that is to say, all their descendants would be equally awnless.
Hence a mutation is definitely a change in the hereditary treasure and has to be accounted for by some change in the hereditary substance. Actually most of the important breeding experiments, which have revealed to us the mechanism of heredity, consisted in a careful analysis of the offspring obtained by crossing, according to a preconceived plan, mutated (or, in many cases, multiply mutated) with non-mutated or with differently mutated individuals. On the other hand, by virtue of their breeding true, mutations are a suitable material on which natural selection may work and produce the species as described by Darwin, by eliminating the unfit and letting the fittest survive. In Darwin’s theory, you just have to substitute ‘mutations’ for his ‘slight accidental variations’ (just as quantum theory substitutes ‘quantum jump’ for ‘continuous transfer of energy’). In all other respects little change was necessary in Darwin’s theory, that is, if I am correctly interpreting the view held by the majority of biologists.
Localization, Recessivity and Dominance
We must now review some other fundamental facts and notions about mutations, again in a slightly dogmatic manner, without showing directly how they spring, one by one, from the experimental evidence.
Figure 8: Heterozygous mutant. The cross marks the mutated gene.
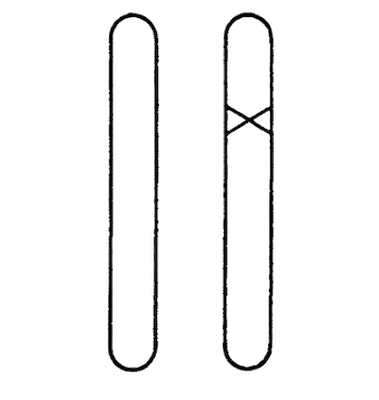
We should expect a definite observed mutation to be caused by a change in a definite region in one of the chromosomes. And so it is. It is important to state that we know definitely, that it is a change in one chromosome only, but not in the corresponding ‘locus’ of the homologous chromosome. Fig. 8 indicates this schematically, the cross denoting the mutated locus. The fact that only one chromosome is affected is revealed when the mutated individual (often called ‘mutant’) is crossed with a non-mutated one. For exactly half of the offspring exhibit the mutant character and half the normal one. That is what is to be expected as a consequence of the separation of the two chromosomes on meiosis in the mutant as shown, very schematically, in Fig. 9. This is a ‘pedigree’, representing every individual (of three consecutive generations) simply by the pair of chromosomes in question. Please realize that if the mutant had both its chromosomes affected, all the children would receive the same (mixed) inheritance, different from that of either parent.
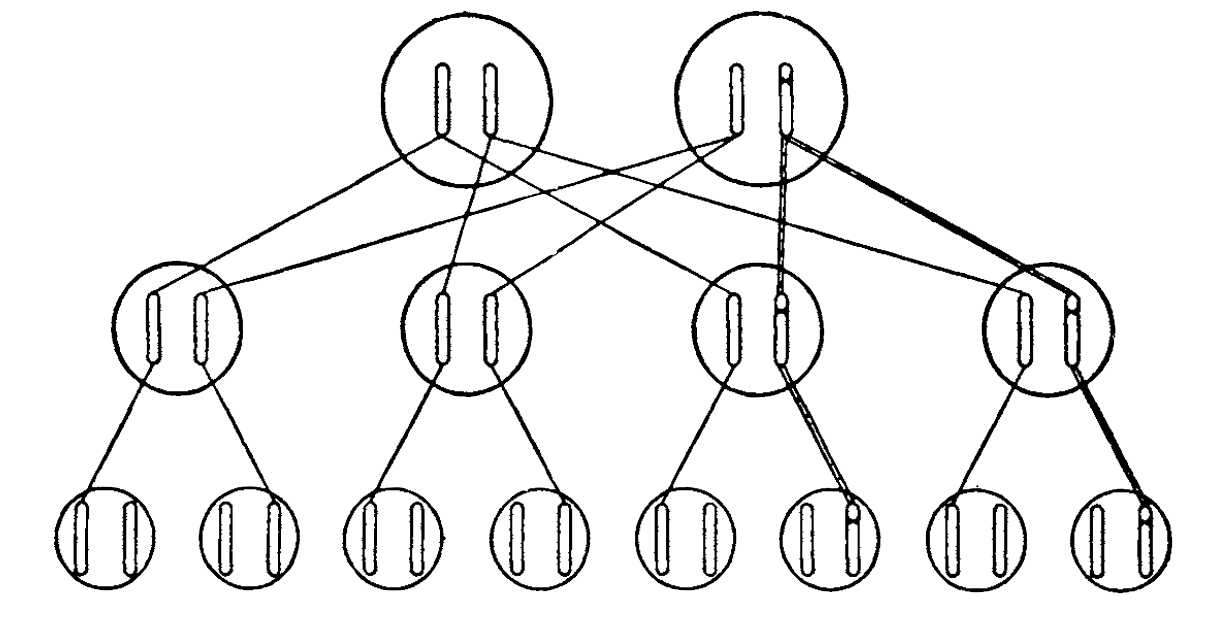
Figure 9: Inheritance of a mutation. The straight lines across indicate the transfer of a chromosome, the double ones that of the mutated chromosome. The unaccounted-for chromosomes of the third generation come from the mates of the second generation, which are not included in the diagram. They are supposed to be non-relatives, free of the mutation.
But experimenting in this domain is not as simple as would appear from what has just been said. It is complicated by the second important fact, viz. that mutations are very often latent. What does that mean? In the mutant the two ‘copies of the code-script’ are no longer identical; they present two different ‘readings’ or ‘versions’, at any rate in that one place. Perhaps it is well to point out at once that, while it might be tempting, it would nevertheless be entirely wrong to regard the original version as ‘orthodox’, and the mutant version as ‘heretic’. We have to is regard them, in principle, as being of equal right – for the normal characters have also arisen from mutations.
What actually happens is that the ‘pattern’ of the individual, as a general rule, follows either the one or the other version, which may be the normal or the mutant one. The version which is followed is called dominant, the other, recessive; in other words, the mutation is called dominant or recessive, according to whether it is immediately effective in changing the pattern or not.
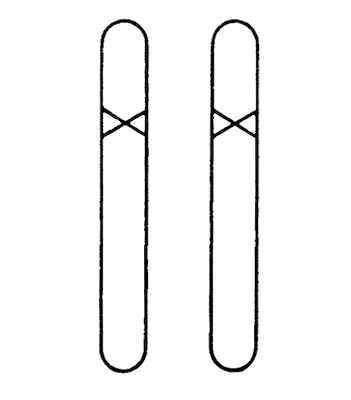
Recessive mutations are even more frequent than dominant ones and are very important, though at first they do not show up at all. To affect the pattern, they have to be present in both chromosomes (see Fig. 10). Such individuals can be produced when two equal recessive mutants happen to be crossed with each other or when a mutant is crossed with itself; this is possible in hermaphroditic plants and even happens spontaneously. An easy reflection shows that in these cases about one-quarter of the offspring will be of this type and thus visibly exhibit the mutated pattern.
Figure 10: Homozygous mutant, obtained in one-quarter of the descendants either from self-fertilization of a heterozygous mutant (see Fig. 8)
or from crossing two of them.
Introducing Some Technical Language
I think it will make for clarity to explain here a few technical terms. For what I called ‘version of the code-script’ – be it the original one or a mutant one – the term ‘allele’ has been adopted. When the versions are different, as indicated in Fig. 8, the individual is called heterozygous, with respect to that locus. When they are equal, as in the non-mutated individual or in the case of Fig. 10, they are called homozygous. Thus a recessive allele influences the pattern only when homozygous, whereas a dominant allele produces the same pattern, whether homozygous or only heterozygous.
Colour is very often dominant over lack of colour (or white). Thus, for example, a pea will flower white only when it has the ‘recessive allele responsible for white’ in both chromosomes in question, when it is ‘homozygous for white’; it will then breed true, and all its descendants will be white. But one ‘red allele’ (the other being white; ‘heterozygous’) will make it flower red, and so will two red alleles (‘homozygous’). The difference of the latter two cases will only show up in the offspring, when the heterozygous red will produce some white descendants, and the homozygous red will breed true.
The fact that two individuals may be exactly alike in their outward appearance, yet differ in their inheritance, is so important that an exact differentiation is desirable. The geneticist says they have the same phenotype, but different genotype. The contents of the preceding paragraphs could thus be summarized in the brief, but highly technical statement: A recessive allele influences the phenotype only when the genotype is homozygous. We shall use these technical expressions occasionally, but shall recall their meaning to the reader where necessary.
The Harmful Effect of Close-Breeding
Recessive mutations, as long as they are only heterozygous, are of course no working-ground for natural selection. If they are detrimental, as mutations very often are, they will nevertheless not be eliminated, because they are latent. Hence quite a host of unfavourable mutations may accumulate and do no immediate damage. But they are, of course, transmitted to that half of the offspring, and that has an important application to man, cattle, poultry or any other species, the good physical qualities of which are of immediate concern to us. In Fig. 9 it is assumed that a male individual (say, for concreteness, myself) carries such a recessive detrimental mutation heterozygously, so that it does not show up. Assume that my wife is free of it. Then half of our children (second line) will also carry it – again heterozygously. If all of them are again mated with non-mutated partners (omitted from the diagram, to avoid reed confusion), a quarter of our grandchildren, on the average, will be affected in the same way.
No danger of the evil ever becoming manifest arises, unless equally affected individuals are crossed with each other, when, as an easy reflection shows, one-quarter of their children, being homozygous, would manifest the damage. Next to self-fertilization (only possible in hermaphrodite plants) the greatest danger would be a marriage between a son and a daughter of mine. Each of them standing an even chance of being latently affected or not, one-quarter of these incestuous unions would be dangerous inasmuch as one-quarter of its children would manifest the damage. The danger factor for an incestuously bred child is thus 1: 16.
In the same way the danger: factor works out to be 1:64 for the offspring of a union between two (‘clean-bred’) grand-children of mine who are first cousins. These do not seem to be overwhelming odds, and actually the second case is usually tolerated. But do not forget that we have analysed the consequences of only one possible latent injury in one partner of the ancestral couple (‘me and my wife’). Actually both of them are quite likely to harbour more than one latent deficiency of this kind. If you know that you yourself harbour a definite one, you have to reckon with 1 out of 8 of your first cousins sharing it! Experiments with plants and animals seem to indicate that in addition to comparatively rare deficiencies of a serious kind, there seem to be a host of minor ones whose chances combine to deteriorate the offspring of close-breeding as a whole. Since we are no longer inclined to eliminate failures in the harsh way the Lacedemonians used to adopt in the Taygetos mountain, we have to take a particularly serious view about these things in the case of man, were natural selection of the fittest is largely retrenched, nay, turned to the contrary. The anti-selective effect of the modern mass slaughter of the healthy youth of all nations is hardly outweighed by the consideration that in more primitive conditions war may have had a positive value in letting the fittest survive.
General and Historical Remarks
The fact that the recessive allele, when heterozygous, is completely overpowered by the dominant and produces no visible effects at all, is amazing. It ought at least to mentioned that there are exceptions to this behaviour. When a homozygous white snapdragon is crossed with, equally homozygous, crimson snapdragon, all the immediate descendants are intermediate in colour, i.e. they are pink (not crimson, as might be expected). A much more important case of two alleles exhibiting their influence simultaneously occurs in blood-groups – but we cannot enter into that here. I should not be astonished if at long last recessivity should turn out to be capable of degrees and to depend on the sensitivity of the tests we apply to examine the ‘phenotype’.
This is perhaps the place for a word on the early history of genetics. The backbone of the theory, the law of inheritance, to successive generations, of properties in which the parents differ, and more especially the important distinction recessive-dominant, are due to the now world famous Augustininan Abbot Gregor Mendel (1822-84). Mendel knew nothing about mutations and chromosomes. In his cloister gardens in Brunn (Brno) he made experiments on the garden pea, of first which he reared different varieties, crossing them and watching their offspring in the 1st, 2nd, 3rd, …, generation. You might say, he experimented with mutants which he found ready-made in nature. The results he published as early as 1866 in the Proceedings of the Naturforschender Verein in Brunn. Nobody seems to have been particularly interested in the abbot’s hobby, and nobody, certainly, had the faintest idea that his discovery would in the twentieth century become the lodestar of an entirely new branch of science, easily the most interesting of our days. His paper was forgotten and was only rediscovered in 1900, simultaneously and independently, by Correns (Berlin), de Vries (Amsterdam) and Tschermaks (Vienna).
The Necessity of Mutation Being a Rare Event
So far we have tended to fix our attention on harmful mutations, which may be the more numerous; but it must be definitely stated that we do encounter advantageous mutations as well. If a spontaneous mutation is a small step in the development of the species, we get the impression that some change is ‘tried out’ in rather a haphazard fashion at the risk of its being injurious, in which case it is automatically eliminated. This brings out one very important point. In order to be suitable material for the work of natural selection, mutations must be rare events, as they actually are. If they were so frequent that there was a considerable chance of, say, a dozen of different mutations occurring in the same individual, the injurious ones would, as a rule, predominate over the advantageous ones and the species, instead of being improved by selection, would remain unimproved, or would perish. The comparative conservatism which results from the high degree of permanence of the genes is essential. An analogy might be sought in the working of a large manufacturing plant in a factory. For developing better methods, innovations, even if as yet unproved, must be tried out. But in order to ascertain whether the innovations improve or decrease the output, it is essential that they should be introduced one at a time, while all the other parts of the mechanism are kept constant.
Mutations Induced by X-Rays
We now have to review a most ingenious series of genetical research work, which will prove to be the most relevant feature of our analysis. The percentage of mutations in the offspring, the so-called mutation rate, can be increased to a high multiple of the small natural mutation rate by irradiating the parents with X-rays or γ-rays. The mutations produced in this way differ in no way (except by being more numerous) from those occurring spontaneously, and one has the impression that every ‘natural’ mutation can also be induced by X-rays. In Drosophila many special mutations recur spontaneously again and again in the vast cultures; they have been located in the chromosome, as described on pp. 26-9, and have been given special names. There have been found even what are called ‘multiple alleles’, that is to say, two or more different ‘versions’ and ‘readings’ – in addition to the normal, non-mutated one – of the same place in the chromosome code; that means not only two, but three or more alternatives in that particular one ‘locus’, any two of which are to each other in the relation ‘dominant-recessive’ when they occur simultaneously in their corresponding loci of the two homologous chromosomes.
The experiments on X-ray-produced mutations give the impression that every particular ‘transition’, say from the normal individual to a particular mutant, or conversely, has its individual ‘X-ray coefficient’, indicating the percentage of the offspring which turns out to have mutated in that particular way, when a unit dosage of X-ray has been applied to the parents, before the offspring was engendered.
First Law. Mutation is a Single Event
Furthermore, the laws governing the induced mutation rate are extremely simple and extremely illuminating. I follow here the report of N. W. Timofeeff, in Biological Reviews, vol. IX, 1934. To a considerable extent it refers to that author’s own beautiful work. The first law is
(1) The increase is exactly proportional to the dosage of rays, so that one can actually speak (as I did) of a coefficient of increase.
We are so used to simple proportionality that we are liable to underrate the far-reaching consequences of this simple law. To grasp them, we may remember that the price of a commodity, for example, is not always proportional to its amount. In ordinary times a shopkeeper may be so much impressed by your having bought six oranges from him, that, on your deciding to take after all a whole dozen, he may give it to you for less than double the price of the six. In times of scarcity the opposite may happen. In the present case, we conclude that the first half-dosage of radiation, while causing, say, one out of a thousand descendants to mutate, has not influenced the rest at all, either in the way of predisposing them for, or of immunizing them against, mutation. For otherwise the second half-dosage would not cause again just one out of a thousand to mutate. Mutation is thus not an accumulated effect, brought about by consecutive small portions of radiation reinforcing each other. It must consist in some single event occurring in one chromosome during irradiation. What kind of event?
Second Law. Localization of the Event
This is answered by the second law, viz.
(2) If you vary the quality of the rays (wave-length) within wide limits, from soft X-rays to fairly hard γ-rays, the coefficient remains constant, provided you give the same dosage in so-called r-units, that is to say, provided you measure the dosage by the total amount of ions produced per unit volume in a suitably chosen standard substance during the time and at the place where the parents are exposed to the rays.
As standard substance one chooses air not only for convenience, but also for the reason that organic tissues are composed of elements of the same atomic weight as air. A lower limit for the amount of ionizations or allied processes (excitations) in the tissue is obtained simply by multiplying the number of ionizations in air by the ratio of the densities. It is thus fairly obvious, and is confirmed by a more critical investigation, that the single event, causing a mutation, is just an ionization (or similar process) occurring within some ‘critical’ volume of the germ cell. What is the size of this critical volume? It can be estimated from the observed mutation rate by a consideration of this kind: if a dosage of 50,000 ions per ${cm}^3$ produces a chance of only 1:1000 for any particular gamete (that finds itself in the irradiated district) to mutate in that particular way, we conclude that the critical volume, the ‘target’ which has to be ‘hit’ by an ionization for that mutation to occur, is only 1/1000 of 1/50000 of a ${cm}^3$, that is to say, one fifty-millionth of a ${cm}^3$. The numbers are not the right ones, but are used only by way of illustration. In the actual estimate we follow M. Delbruck, in a paper by Delbruck, N.W. Timofeeff and K.G. Zimmer, which will also be the principal source of the theory to be expounded in the following two chapters. He arrives there at a size of only about ten average atomic distances cubed, containing thus only about $10^3$ = a thousand atoms. The simplest interpretation of this result is that there is a fair chance of producing that mutation when an ionization (or excitation) occurs not more than about ‘10 atoms away’ from some particular spot in the chromosome. We shall discuss this in more detail presently.
The Timofeeff report contains a practical hint which I cannot refrain from mentioning here, though it has, of course, no bearing on our present investigation. There are plenty of occasions in modern life when a human being has to be exposed to X-rays. The direct dangers involved, as burns, X-ray cancer, sterilization, are well known, and protection by lead screens, lead-loaded aprons, etc., is provided, especially for nurses and doctors who have to handle the rays regularly. The point is, that even when these imminent dangers to the individual are successfully warded off, there appears to be the indirect danger of small detrimental mutations being produced in the germ cells – mutations of the kind envisaged when we spoke of the unfavourable results of close-breeding. To put it drastically, though perhaps a little naively, the injuriousness of a marriage between first cousins might very this well be increased by the fact that their grandmother had served for a long period as an X-ray nurse. It is not a point that need worry any individual personally. But any possibility of gradually infecting the human race with unwanted latent mutations ought to be a matter of concern to the community.
Chapter 4: The Quantum-Mechanical Evidence
Permanence Unexplainable by Classical Physics
Thus, aided by the marvellously subtle instrument of X-rays (which, as the physicist remembers, revealed thirty years ago really the detailed atomic lattice structures of crystals), the united efforts of biologists and physicists have of late succeeded in reducing the upper limit for the size of the microscopic structure, being responsible for a definite large-scale feature of the individual – the ‘size of a gene’ – and reducing it far below the estimates obtained on pp 29-30. We are now seriously faced with the question: How can we, from the point of view of statistical physics, reconcile the facts that the gene structure seems to involve only a comparatively small number of atoms (of the order of 1,000 and possibly much less), and that nevertheless it displays a most regular and lawful activity – with a durability or permanence that borders upon the miraculous?
Let me throw the truly amazing situation into relief once again. Several members of the Habsburg dynasty have a peculiar disfigurement of the lower lip (‘Habsburger Lippe’). Its inheritance has been studied carefully and published, complete with historical portraits, by the Imperial Academy In Vienna, under the auspices of the family. The feature proves to be a genuinely Mendelian ‘allele’ to the normal form of the lip. Fixing our attention on the portraits of a member of the family in the sixteenth century and of his descendant, living in the nineteenth, we may safely assume that the material gene structure, responsible for the abnormal feature, has been carried on from generation to generation through the centuries, faithfully reproduced at every one of the not very numerous cell divisions that lie between. Moreover, the number of atoms involved in the responsible gene structure is likely to be of the same order of magnitude as in the cases tested by X-rays. The gene has been kept at a temperature around 98°F during all that time. How are we to understand that it has remained unperturbed by the disordering tendency of the heat motion for centuries?
A physicist at the end of the last century would have been at a loss to answer this question, if he was prepared to draw only on those laws of Nature which he could explain and which he really understood. Perhaps, indeed, after a short reflection on the statistical situation he would have answered (correctly, as we shall see): These material structures can only be molecules. Of the existence, and sometimes very high stability, of these associations of atoms, chemistry had already acquired a widespread knowledge at the time. But the knowledge was purely empirical. The nature of a molecule was not understood – the strong mutual bond of the atoms which keeps a molecule in shape was a complete conundrum to everybody. Actually, the answer proves to be correct. But it is of limited value as long as the enigmatic biological stability is traced back only to an equally enigmatic chemical stability. The evidence that two features, similar in appearance, are based on the same principle, is always precarious as long as the principle itself is unknown.
Explicable by Quantum Theory
In this case it is supplied by quantum theory. In the light of present knowledge, the mechanism of heredity is closely related to, nay, founded on, the very basis of quantum theory. This theory was discovered by Max Planck in 1900. Modern genetics can be dated from the rediscovery of Mendel’s paper by de Vries, Correns and Tschermak (1900) and from de Vries’s paper on mutations (l901-3). Thus the births of the two great theories nearly coincide, and it is small wonder that both of them had to reach a certain maturity before the connection could emerge. On the side of quantum theory it took more than a quarter of a century till in 1926-7 the quantum theory of the chemical bond was outlined in its general principles by W. Heitler and F. London. The Heitler-London theory involves the most subtle and intricate conceptions of the latest development of quantum theory (called ‘quantum mechanics’ or ‘wave mechanics’). A presentation without the use of calculus is well-nigh impossible or would at least require another little volume like this. But fortunately, now that all work has been done and has served to clarify our thinking, it seems to be possible to point out in a more direct manner the connection between ‘quantum jumps’ and mutations, to pick out at the moment the most conspicuous item. That is what we attempt here.
Quantum Theory – Discrete States – Quantum Jumps
The great revelation of quantum theory was that features of a discreteness were discovered in the Book of Nature, in context in which anything other than continuity seemed to be absurd according to the views held until then.
The first case of this kind concerned energy. A body on the large scale changes its energy continuously. A pendulum, for instance, that is set swinging is gradually slowed down by the resistance of the air. Strangely enough, it proves necessary to admit that a system of the order of the atomic scale behaves differently. On grounds upon which we cannot enter here, we then have to assume that a small system can by its very nature possess only certain discrete amounts of energy, called its peculiar energy levels. The transition from one state to another is a rather mysterious event, which is usually called a ‘quantum jump’.
But energy is not the only characteristic of a system. Take again our pendulum, but think of one that can perform different kinds of movement, a heavy ball suspended by a string from the ceiling. It can be made to swing in a north-south or east-west or any other direction or in a circle or in an ellipse. By gently blowing the ball with a bellows, it can be made to pass continuously from one state of motion to other. For small-scale systems most of these or similar characteristics – we cannot enter into details – change discontinuously. They are ‘quantized’, just as the energy is.
The result is that a number of atomic nuclei, including their bodyguards of electrons, when they find themselves close to each other, forming ‘a system’, are unable by their very nature to adopt any arbitrary configuration we might think of. Their very nature leaves them only a very numerous but discrete series of ‘states’ to choose from. We usually call them levels or energy levels, because the energy is a very relevant part of the characteristic. But it must be understood that the complete description includes much more than just the energy. It is virtually correct to think of a state as meaning a definite configuration of all the corpuscles.
The transition from one of these configurations to another is a quantum jump. If the second one has the greater energy (‘is a higher level’), the system must be supplied from outside with at least the difference of the two energies to make the transition possible. To a lower level it can change spontaneously on the spending the surplus of energy in radiation.
Molecules
Among the discrete set of states of a given selection of atoms there need not necessarily but there may be a lowest level, implying a close approach of the nuclei to each other. Atoms in such a state form a molecule. The point to stress here is, that the molecule will of necessity have a certain stability; the configuration cannot change, unless at least the energy difference, necessary to ‘lift’ it to the next higher level, is supplied from outside. Hence this level difference, which is a well-defined quantity, determines quantitatively the degree of stability of the molecule. It will be observed how intimately this fact is linked with the very basis of quantum theory, viz. with the discreteness of the level scheme.
I must beg the reader to take it for granted that this order of ideas has been thoroughly checked by chemical facts; and that it has proved successful in explaining the basic fact of chemical valency and many details about the structure of molecules, their binding-energies, their stabilities at different temperatures, and so on. I am speaking of the Heitler-London theory, which, as I said, cannot be examined in detail here.
Their Stability Dependent on Temperature
We must content ourselves with examining the point which is of paramount interest for our biological question, namely, the stability of a molecule at different temperatures. Take our system of atoms at first to be actually in its state of lowest energy. The physicist would call it a molecule at the absolute zero of temperature. To lift it to the next higher state or level a definite supply of energy is required. The simplest way of trying to supply it is to ‘heat up’ your molecule. You bring it into an environment of higher temperature (‘heat bath’), thus allowing other systems (atoms, molecules) to impinge upon it. Considering the entire irregularity of heat motion, there is no sharp temperature limit at which the ‘lift’ will be brought about with certainty and immediately. Rather, at any temperature (different from absolute zero) there is a certain smaller or greater chance for the lift to occur, the chance increasing of course with the temperature of the heat bath. The best way to express this chance is to indicate the average time you will have to wait until the lift takes place, the ‘time of expectation’.
From an investigation, due to M. Polanyi and E. Wigner, the ‘time of expectation’ largely depends on the ratio of two energies, one being just the energy difference itself that is required to effect the lift (let us write W for it), the other one characterizing the intensity of the heat motion at the temperature in question (let us write T for the absolute temperature and kT for the characteristic energy). It stands to reason that the chance for effecting the lift is smaller, and hence that the time of expectation is longer, the higher the lift itself compared with the average heat energy, that is to say, the greater the ratio W:kT. What is amazing is how enormously the time of expectation depends on comparatively small changes of the ratio W:kT. To give an example (following Delbruck): for W 30 times kT the time of expectation might be as short as 1\10 s., but would rise to 16 months when W is 50 times kT, and to 30,000 years when W is 60 times kT!
Mathematical Interlude
It might be as well to point out in mathematical language – for those readers to whom it appeals – the reason for this enormous sensitivity to changes in the level step or temperature, and to add a few physical remarks of a similar kind. The reason is that the time of expectation, call it t, depends on the ratio W/kT by an exponential function, thus
\[t = \tau e^{W/kT}\]$\tau$ is a certain small constant of the order of $10^{-13}$ or $10^{-14}$s. Now, this particular exponential function is not an accidental feature. It recurs again and again in the statistical theory of heat, forming, as it were, its backbone. It is a measure of the improbability of an energy amount as large as W gathering accidentally in some particular part of the system, and it is this improbability which increases so enormously when a considerable multiple of the ‘average energy’ kT is required.
Actually a W = 30kT (see the example quoted above) is already extremely rare. That it does not yet lead to an enormously long time of expectation (only 1/10s. in our example) is, of course, due to the smallness of the factor $\tau$. This factor has a physical meaning. It is of the order of the period of the vibrations which take place in the system all the time. You could, very broadly, describe this factor as meaning that the chance of accumulating the required amount W, though very small, recurs again and again ‘at every vibration’, that is to say, about $10^{13}$ or $10^{14}$ times during every second.
First Amendment
In offering these considerations as a theory of the stability of the molecule it has been tacitly assumed that the quantum jump which we called the ‘lift’ leads, if not to a complete disintegration, at least to an essentially different configuration of the same atoms – an isomeric molecule, as the chemist would say, that is, a molecule composed of the same atoms in a different arrangement (in the application to biology it is going to represent a different ‘allele’ in the same ‘locus’ and the quantum jump will represent a mutation).
To allow of this interpretation two points must be amended in our story, which I purposely simplified to make it at all intelligible. From the way I told it, it might be imagined that only in its very lowest state does our group of atoms form what we call a molecule and that already the next higher state is ‘something else’. That is not so. Actually the lowest level is followed by a crowded series of levels which do not involve any appreciable change in the configuration as a whole, but only correspond to those small vibrations among the atoms which we have mentioned above. They, too, are ‘quantized’, but with comparatively small steps from one level to the next. Hence the impacts of the particles of the ‘heat bath’ may suffice to set them up already at fairly low temperature. If the molecule is an extended structure, you may conceive these vibrations as high-frequency sound waves, crossing the molecule without doing it any harm.
So the first amendment is not very serious: we have to disregard the ‘vibrational fine-structure’ of the level scheme. The term ‘next higher level’ has to be understood as meaning the next level that corresponds to a relevant change of configuration.
Second Amendment
The second amendment is far more difficult to explain, because it is concerned with certain vital, but rather complicated, features of the scheme of relevantly different levels. The free passage between two of them may be obstructed, quite apart from the required energy supply; in fact, it may be obstructed even from the higher to the lower state.
Let us start from the empirical facts. It is known to the chemist that the same group of atoms can unite in more than one way to form a molecule. Such molecules are called isomeric (‘consisting of the same parts’). Isomerism is not an exception, it is the rule. The larger the molecule, the more isomeric alternatives are offered. Fig. 11 shows one of the simplest cases, the two kinds of propyl alcohol, both consisting of 3 carbons (C), 8 hydrogens (H), 1 oxygen (O). The latter can be interposed between any hydrogen and its carbon, but only the two cases shown in our figure are different substances. And they really are. All their physical and chemical constants are distinctly different. Also their energies are different, they represent ‘different levels’.
Figure 11: The two isomers of propyl-alcohol.
The remarkable fact is that both molecules are perfectly stable, both behave as though they were ‘lowest states’. There are no spontaneous transitions from either state towards the other. The reason is that the two configurations are not neighbouring configurations. The transition from one to the other can only take place over intermediate configurations which have a greater energy than either of them. To put it crudely, the oxygen has to be extracted from one position and has to be inserted into the other. There does not seem to be a way of doing that without passing through configurations of considerably higher energy. The state of affairs is sometimes figuratively pictured as in Fig. 12, in which 1 and 2 represent the two isomers, 3 the ‘threshold’ between them, and the two arrows indicate the ‘lifts’, that is to say, the energy supplies required to produce the transition from state 1 to state 2 or from state 2 to state 1, respectively.
Figure 12: Energy threshold (3) between the isomeric levels (1) and (2). The arrows indicate the minimum energies required for transition.
Now we can give our ‘second amendment’, which is that transitions of this ‘isomeric’ kind are the only ones in which we shall be interested in our biological application. It was these we had in mind when explaining ‘stability’ on pp. 49-51. The ‘quantum jump’ which we mean is the transition from one relatively stable molecular configuration to another. The energy supply required for the transition (the quantity denoted by W) is not the actual level difference, but the step from the initial level up to the threshold (see the arrows in Fig. 12). Transitions with no threshold interposed between the initial and the final state are entirely uninteresting, and that not only in our biological application. They have actually nothing to contribute to the chemical stability of the molecule. Why? They have no lasting effect, they remain unnoticed. For, when they occur, they are almost immediately followed by a relapse so into the initial state, since nothing prevents their return.
Chapter 5: Delbruck’s Model Discussed and Tested
The General Picture of the Hereditary Substance
From these facts emerges a very simple answer to our question, namely: Are these structures, composed of comparatively few atoms, capable of withstanding for long periods the disturbing influence of heat motion to which the hereditary substance is continually exposed? We shall assume the structure of a gene to be that of a huge molecule, capable only of discontinuous change, which consists in a rearrangement of the atoms and leads to an isomeric molecule. The rearrangement may affect only a small region of the gene, and a vast number of different rearrangements may be possible. The energy thresholds, separating the actual configuration from any possible isomeric ones, have to be high enough (compared with the average heat energy of an atom) to make the change-over a rare event. These rare events we shall identify with spontaneous mutations.
The later parts of this chapter will be devoted to putting this general picture of a gene and of mutation (due mainly to the German physicist M. Delbruck) to the test, by comparing it in detail with genetical facts. Before doing so, we may fittingly make some comment on the foundation and general nature of the theory.
The Uniqueness of the Picture
Was it absolutely essential for the biological question to dig up the deepest roots and found the picture on quantum mechanics? The conjecture that a gene is a molecule is today, I dare say, a commonplace. Few biologists, whether familiar with quantum theory or not, would disagree with it. On p. 47 we ventured to put it into the mouth of a pre-quantum physicist, as the only reasonable explanation of the observed permanence. The subsequent considerations about isomerism, threshold energy, the paramount role of the ratio W:kT in determining the probability of an isomeric transition – all that could very well be introduced on a purely empirical basis, at any rate without drawing on quantum theory. Why did I so strongly insist on the quantum-mechanical point of view, though I could not really make it clear in this little book and may well have bored many a reader?
Quantum mechanics is the first theoretical aspect which accounts from first principles for all kinds of aggregates of atoms actually encountered in Nature. The Heitler-London bondage is a unique, singular feature of the theory, not invented for the purpose of explaining the chemical bond. It comes in quite by itself, in a highly interesting and puzzling manner, being forced upon us by entirely different considerations. It proves to correspond exactly with the observed chemical facts, and, as I said, it is a unique feature, well enough understood to tell with reasonable certainty that ‘such a thing could not happen again’ in the further development of quantum theory.
Consequently, we may safely assert that there is no alternative to the molecular explanation of the hereditary substance. The physical aspect leaves no other possibility to account for itself and of its permanence. If the Delbruck picture should fail, we would have to give up further attempts. That is the first point I wish to make.
Some Traditional Misconceptions
But it may be asked: Are there really no other endurable structures composed of atoms except molecules? Does not a gold coin, for example, buried in a tomb for a couple of thousand years, preserve the traits of the portrait stamped on it? It is true that the coin consists of an enormous number of atoms, but surely we are in this case not inclined to attribute the mere preservation of shape to the statistics of large numbers. The same remark applies to a neatly developed batch of crystals we find embedded in a rock, where it must have been for geological periods without changing.
That leads us to the second point I want to elucidate. The cases of a molecule, a solid, a crystal are not really different. In the light of present knowledge they are virtually the same. Unfortunately, school teaching keeps up certain traditional views, which have been out of date for many years and which obscure the understanding of the actual state of affairs.
Indeed, what we have learnt at school about molecules does not give the idea that they are more closely akin to the solid state than to the liquid or gaseous state. On the contrary, we have been taught to distinguish carefully between a physical change, such as melting or evaporation in which the molecules are preserved (so that, for example, alcohol, whether solid, liquid or a gas, always consists of the same molecules, $C_2H_6O$), and a chemical change, as, for example, the burning of alcohol, $C_2H_6O + 30_2 = 2C0_2 + 3H_2O$, where an alcohol molecule and three oxygen molecules undergo a rearrangement to form two molecules of carbon dioxide and three molecules of water.
About crystals, we have been taught that they form three-fold periodic lattices, in which the structure of the single molecule is sometimes recognizable, as in the case of alcohol, and most organic compounds, while in other crystals, e.g. rock-salt (NaCl), NaCl molecules cannot be unequivocally delimited, because every Na atom is symmetrically surrounded by six Cl atoms, and vice versa, so that it is largely arbitrary what pairs, if any, are regarded as molecular partners.
Finally, we have been told that a solid can be crystalline or not, and in the latter case we call it amorphous.
Different ‘States’ of Matter
Now I would not go so far as to say that all these statements and distinctions are quite wrong. For practical purposes they are sometimes useful. But in the true aspect of the structure of matter the limits must be drawn in an entirely different way. The fundamental distinction is between the two lines of the following scheme of ‘equations’:
- molecule = solid = crystal.
- gas = liquid = amorphous.
We must explain these statements briefly. The so-called amorphous solids are either not really amorphous or not really solid. In ‘amorphous’ charcoal fibre the rudimentary structure of the graphite crystal has been disclosed by X-rays. So charcoal is a solid, but also crystalline. Where we find no crystalline structure we have to regard the thing as a liquid with very high ‘viscosity’ (internal friction). Such a substance discloses by the absence of a well-defined melting temperature and of a latent heat of melting that it is not a true solid. When heated it softens gradually and eventually liquefies without discontinuity. (I remember that at the end of the first Great War we were given in Vienna an asphalt-like substance as a substitute for coffee. It was so hard that one had to use a chisel or a hatchet to break the little brick into pieces, when it would show a smooth, shell-like cleavage. Yet, given time, it would behave as a liquid, closely packing the lower part of a vessel in which you were unwise enough to leave it for a couple of days.).
The continuity of the gaseous and liquid state is a well-known story. You can liquefy any gas without discontinuity by taking your way ‘around’ the so-called critical point. But we shall not enter on this here.
The Distinction That Really Matters
We have thus justified everything in the above scheme, except the main point, namely, that we wish a molecule to be regarded as a solid = crystal.
The reason for this is that the atoms forming a molecule, whether there be few or many of them, are united by forces of exactly the same nature as the numerous atoms which build up a true solid, a crystal. The molecule presents the same solidity of structure as a crystal. Remember that it is precisely this solidity on which we draw to account for the permanence of the gene!
The distinction that is really important in the structure of small matter is whether atoms are bound together by those ‘solidifying’ Heitler-London forces or whether they are not. In a solid and in a molecule they all are. In a gas of single atoms (as e.g. think mercury vapour) they are not. In a gas composed of molecules, only the atoms within every molecule are linked in this way.
The Aperiodic Solid
A small molecule might be called ‘the germ of a solid’. Starting from such a small solid germ, there seem to be two different ways of building up larger and larger associations. One is the comparatively dull way of repeating the same structure in three directions again and again. That is the way followed in a growing crystal. Once the periodicity is established, there is no definite limit to the size of the aggregate. The other way is that of building up a more and more extended aggregate without the dull device of repetition. That is the case of the more and more complicated organic molecule in which every atom, and every group of atoms, plays an individual role, not entirely equivalent to that of many others (as is the case in a periodic structure). We might quite properly call that an aperiodic crystal or solid and express our hypothesis by saying: We believe a gene – or perhaps the whole chromosome fibre – to be an aperiodic solid.
The Variety of Contents Compressed in the Miniature Code
It has often been asked how this tiny speck of material, nucleus of the fertilized egg, could contain an elaborate code-script involving all the future development of the organism. A well-ordered association of atoms, endowed with sufficient resistivity to keep its order permanently, appears to be the only conceivable material structure that offers a variety of possible (‘isomeric’) arrangements, sufficiently large to embody a complicated system of ‘determinations’ within a small spatial boundary. Indeed, the number of atoms in such a structure need not be very large to produce an almost unlimited number of possible arrangements. For illustration, think of the Morse code. The two different signs of dot and dash in well-ordered groups of not more than four allow thirty different specifications. Now, if you allowed yourself the use of a third sign, in addition to dot and dash, and used groups of not more than ten, you could form 88,572 different ‘letters’; with five signs and groups up to 25, the number is 372,529,029,846,191,405.
It may be objected that the simile is deficient, because our two Morse signs may have different composition (e.g. .--and ..-) and thus they are a bad analogue for isomerism. To remedy this defect, let us pick, from the third example, only the combinations of exactly 25 symbols and only those containing exactly 5 out of each of the supposed 5 types (5 dots, 5 dashes, etc.). A rough count gives you the number of combinations as more 62,330,000,000,000, where zeros on the right stand for figures which I have not taken the trouble to compute.
Of course, in the actual case, by no means ‘every’ arrangement of the group of atoms will represent a possible molecule; moreover, it is not a question of a code to be adopted arbitrarily, for the code-script must itself be the operative factor bringing about the development. But, on the other hand, the number chosen in the example (25) is still very small, and we have envisaged only the simple arrangements in one line. What we wish to illustrate is simply that with the molecular picture of the gene it is no longer inconceivable that the miniature code should precisely correspond with a highly complicated and specified plan of development and should somehow contain the means to put it into operation.
Comparison With Facts: Degree of Stability; Discontinuity of Mutations
Now let us at last proceed to compare the theoretical picture with the biological facts. The first question obviously is, whether it can really account for the high degree of permanence we observe. Are threshold values of the required amount – high multiples of the average heat energy $kT$ – reasonable, are they within the range known from ordinary chemistry? That question is trivial; it can be answered in the affirmative without inspecting tables. The molecules of any substance which the chemist is able to isolate at a given temperature must at that temperature have a lifetime of at least minutes. (That is putting it mildly; as a rule they have much more.) Thus the threshold values the chemist encounters are of necessity precisely of the order of magnitude required to account for practically any degree of permanence the biologist may encounter; for we recall from p. 51 that thresholds varying within a range of about 1:2 will account for lifetimes ranging from a fraction of a second to tens of thousands of years.
But let me mention figures, for future reference. The ratios $W/kT$ mentioned by way of example on p. 51, viz. $W/kT = 30,50,60,$ producing lifetimes of 1/10 s, 16 months, 30,000 years, respectively, correspond at room temperature with threshold values of 0.9, 1.5, 1.8 electron-volts.
We must explain the unit ‘electron-volt’, which is rather convenient for the physicist, because it can be visualized. For example, the third number (1.8) means that an electron, accelerated by a voltage of about 2 volts, would have acquired just sufficient energy to effect the transition by impact. (For comparison, the battery of an ordinary pocket flash-light has 3 volts.).
These considerations make it conceivable that an isomeric change of configuration in some part of our molecule is, produced by a chance fluctuation of the vibrational energy, can actually be a sufficiently rare event to be interpreted as a spontaneous mutation. Thus we account, by the very principles of quantum mechanics, for the most amazing fact about mutations, the fact by which they first attracted de Vrie’s attention, namely, that they are ‘jumping’ variations, no intermediate forms occurring.
Stability of Naturally Selected Genes
Having discovered the increase of the natural mutation rate by any kind of ionizing rays, one might think of attributing the natural rate to the radio-activity of the soil and air and to cosmic radiation. But a quantitative comparison with the X-ray results shows that the ‘natural radiation’ is much too weak and could account only for a small fraction of the natural rate. Granted that we have to account for the rare natural mutations by chance fluctuations of the heat motion, we must not be very much astonished that Nature has succeeded in making such a subtle choice of threshold values as is necessary to make mutation rare. For we have, earlier in these lectures, arrived at the conclusion that frequent mutations are detrimental to evolution. Individuals which, by mutation, acquire a gene configuration of insufficient stability, will have little chance of seeing their ‘ultra-radical’, rapidly mutating descendancy survive long. The species will be freed of them and will thus collect stable genes by natural selection.
The Sometimes Lower Stability of Mutants
But, of course, as regards the mutants which occur in our breeding experiments and which we select, qua mutants, for studying their offspring, there is no reason to expect that they should all show that very high stability. For they have not yet been ‘tried out’ – or, if they have, they have been ‘rejected’ in the wild breeds – possibly for too high mutability. At any rate, we are not at all astonished to learn that actually some of these mutants do show a much higher mutability than the normal ‘wild’ genes.
Temperature Influences Unstable Genes Less Than Stable Ones
This enables us to test our mutability formula, which was
\[t=\tau e^{W/kT}\](It will be remembered that t is the time of expectation for a mutation with threshold energy W.) We ask: How does $t$ change with the temperature? We easily find from the preceding formula in good approximation the ratio of the value of $t$ at temperature $T + 10$ to that at temperature $T$.
\[\frac{t_{T+10}}{t_{T}}= e^{-10W/kT^2}\]The exponent being now negative, the ratio is, naturally, there smaller than 1. The time of expectation is diminished by raising the temperature, the mutability is increased. Now that can be tested and has been tested with the fly Drosophila in the range of temperature which the insects will stand. The result was, at first sight, surprising. The low mutability of wild genes was distinctly increased, but the comparatively high mutability occurring with some of the already mutated genes was not, or at any rate was much less, increased. That is just what we expect on comparing our two formulae. A large value of $W/kT$, which according to the first formula is required to make $t$ large (stable gene), will, according to the second one, make for a small value of the ratio computed there, that is to say for a considerable increase of mutability with temperature. (The actual values of the ratio seem to lie between about 1/2 and 1/5. The reciprocal, 2.5, is what in an ordinary chemical reaction we call the van’t Hoff factor.)
How X-Rays Produce Mutation
Turning now to the X-ray-induced mutation rate, we have already inferred from the breeding experiments, first (from the proportionality of mutation rate, and dosage), that some single event produces the mutation; secondly (from quantitative results and from the fact that the mutation rate is determined by the integrated ionization density and independent of the wave-length), that this single event must be an ionization, or similar process, which has to take place inside a certain volume of only about 10 atomic-distances-cubed, in order to produce a specified mutation. According to our picture, the energy for overcoming the threshold must obviously be furnished by that explosion-like process, ionization or excitation. I call it explosion-like, because the energy spent in one ionization (spent, incidentally, not by the X-ray itself, but by a secondary electron it produces) is well known and has the comparatively enormous amount of 30 electron-volts. It is bound to be turned into enormously increased heat motion around the point where it is discharged and to spread from there in the form of a ‘heat wave’, a wave of intense oscillations of the atoms. That this heat wave should still be able to furnish the required threshold energy of 1 or 2 electron-volts at an average ‘range of action’ of about ten atomic distances, is not inconceivable, though it may well be that an unprejudiced physicist might have anticipated a slightly lower range of action. That in many cases the effect of the explosion will not be an orderly isomeric transition but a lesion of the chromosome, a lesion that becomes lethal when, by ingenious crossings, the uninjured partner (the corresponding chromosome of the second set) is removed and replaced by a partner whose corresponding gene is known to be itself morbid – all that is absolutely to be expected and it is exactly what is observed.
Their Efficiency Does Not Depend on Spontaneous Mutability
Quite a few other features are, if not predictable from the picture, easily understood from it. For example, an unstable mutant does not on the average show a much higher X-ray mutation rate than a stable one. Now, with an explosion furnishing an energy of 30 electron-volts you would certainly not expect that it makes a lot of difference whether the required threshold energy is a little larger or a little smaller, say 1 or 1.3 volts.
Reversible Mutations
In some cases a transition was studied in both directions, say from a certain ‘wild’ gene to a specified mutant and back from that mutant to the wild gene. In such cases the natural mutation rate is sometimes nearly the same, sometimes very different. At first sight one is puzzled, because the threshold to be overcome seems to be the same in both cases. But, of course, it need not be, because it has to be measured from the energy level of the starting configuration, and that may be different for the wild and the mutated gene. (See Fig. 12 on p. 54, where ‘1’ might refer to the wild allele, ‘2’ to the mutant, whose lower stability would be indicated by the shorter arrow.)
On the whole, I think, Delbruck’s ‘model’ stands the tests fairly well and we are justified in using it in further considerations.
Chapter 6: Order, Disorder and Entropy
A Remarkable General Conclusion From the Model
Let me refer to the phrase on p. 62, in which I tried to explain that the molecular picture of the gene made it at least conceivable that the miniature code should be in one-to-one correspondence with a highly complicated and specified plan of development and should somehow contain the means of putting it into operation. Very well then, but how does it do this? How are we going to turn ‘conceivability’ into true understanding?
Delbruck’s molecular model, in its complete generality, seems to contain no hint as to how the hereditary substance works. Indeed, I do not expect that any detailed information on this question is likely to come from physics in the near future. The advance is proceeding and will, I am sure, continue to do so, from biochemistry under the guidance of physiology and genetics.
No detailed information about the functioning of the genetical mechanism can emerge from a description of its structure so general as has been given above. That is obvious. But, strangely enough, there is just one general conclusion to be obtained from it, and that, I confess, was my only motive for writing this book.
From Delbruck’s general picture of the hereditary substance it emerges that living matter, while not eluding the ‘laws of physics’ as established up to date, is likely to involve ‘other laws of physics’ hitherto unknown, which, however, once they have been revealed, will form just as integral a part of this science as the former.
Order Based on Order
This is a rather subtle line of thought, open to misconception in more than one respect. All the remaining pages are concerned with making it clear. A preliminary insight, rough but not altogether erroneous, may be found in the following considerations: It has been explained in chapter 1 that the laws of physics, as we know them, are statistical laws. They have a lot to do with the natural tendency of things to go over into disorder.
But, to reconcile the high durability of the hereditary substance with its minute size, we had to evade the tendency to disorder by ‘inventing the molecule’, in fact, an unusually large molecule which has to be a masterpiece of highly differentiated order, safeguarded by the conjuring rod of quantum theory. The laws of chance are not invalidated by this ‘invention’, but their outcome is modified. The physicist is familiar with the fact that the classical laws of physics are modified by quantum theory, especially at low temperature. There are many instances of this. Life seems to be one of them, a particularly striking one. Life seems to be orderly and lawful behaviour of matter, not based exclusively on its tendency to go over from order to disorder, but based partly on existing order that is kept up.
To the physicist – but only to him – I could hope to make my view clearer by saying: The living organism seems to be a macroscopic system which in part of its behaviour approaches to that purely mechanical (as contrasted with thermodynamical) conduct to which all systems tend, as the temperature approaches absolute zero and the molecular disorder is removed.
The non-physicist finds it hard to believe that really the ordinary laws of physics, which he regards as the prototype of inviolable precision, should be based on the statistical tendency of matter to go over into disorder. I have given examples in chapter 1. The general principle involved is the famous Second Law of Thermodynamics (entropy principle) and its equally famous statistical foundation. On pp. 69-74 I will try to sketch the bearing of the entropy principle on the large-scale behaviour of a living organism – forgetting at the moment all that is known about chromosomes, inheritance, and so on.
Living Matter Evades the Decay to Equilibrium
What is the characteristic feature of life? When is a piece of matter said to be alive? When it goes on ‘doing something’, moving, exchanging material with its environment, and so forth, and that for a much longer period than we would expect of an inanimate piece of matter to ‘keep going’ under similar circumstances. When a system that is not alive is isolated or placed in a uniform environment, all motion usually comes to a standstill very soon as a result of various kinds of friction; differences of electric or chemical potential are equalized, substances which tend to form a chemical compound do so, temperature becomes uniform by heat conduction. After that the whole system fades away into a dead, inert lump of matter. A permanent state is reached, in which no observable events occur. The physicist calls this the state of thermodynamical equilibrium, or of ‘maximum entropy’.
Practically, a state of this kind is usually reached very rapidly. Theoretically, it is very often not yet an absolute equilibrium, not yet the true maximum of entropy. But then the final approach to equilibrium is very slow. It could take anything between hours, years, centuries,… To give an example – one in which the approach is still fairly rapid: if a glass filled with pure water and a second one filled with sugared water are placed together in a hermetically closed case at constant temperature, it appears at first that nothing happens, and the impression of complete equilibrium is created. But after a day or so it is noticed that the pure water, owing to its higher vapour pressure, slowly evaporates and condenses on the solution. The latter overflows. Only after the pure water has totally evaporated has the sugar reached its aim of being equally distributed among all the liquid water available.
These ultimate slow approaches to equilibrium could never be mistaken for life, and we may disregard them here. I have referred to them in order to clear myself of a charge of inaccuracy.
It Feeds on ‘Negative Entropy’
It is by avoiding the rapid decay into the inert state of ‘equilibrium’ that an organism appears so enigmatic; so much so, that from the earliest times of human thought some special non-physical or supernatural force (vis viva, entelechy) was claimed to be operative in the organism, and in some quarters is still claimed.
How does the living organism avoid decay? The obvious answer is: By eating, drinking, breathing and (in the case of plants) assimilating. The technical term is metabolism. The Greek word means change or exchange. Exchange of what? Originally the underlying idea is, no doubt, exchange of material. (E.g. the German for metabolism is Stoffwechsel.) That the exchange of material should be the essential thing is absurd. Any atom of nitrogen, oxygen, sulphur, etc., is as good as any other of its kind; what could be gained by exchanging them? For a while in the past our curiosity was silenced by being told that we feed upon energy. In some very advanced country (I don’t remember whether it was Germany or the U.S.A. or both) you could find menu cards in restaurants indicating, in addition to the price, the energy content of every dish. Needless to say, taken literally, this is just as absurd. For an adult organism the energy content is as stationary as the material content. Since, surely, any calorie is worth as much as any other calorie, one cannot see how a mere exchange could help.
What then is that precious something contained in our food which keeps us from death? That is easily answered. Every process, event, happening – call it what you will; in a word, everything that is going on in Nature means an increase of the entropy of the part of the world where it is going on. Thus a living organism continually increases its entropy – or, as you may say, produces positive entropy – and thus tends to approach the dangerous state of maximum entropy, which is of death. It can only keep aloof from it, i.e. alive, by continually drawing from its environment negative entropy – which is something very positive as we shall immediately see. What an organism feeds upon is negative entropy. Or, to put it less paradoxically, the essential thing in metabolism is that the organism succeeds in freeing itself from all the entropy it cannot help producing while alive.
What is Entropy?
What is entropy? Let me first emphasize that it is not a hazy concept or idea, but a measurable physical quantity just like of the length of a rod, the temperature at any point of a body, the heat of fusion of a given crystal or the specific heat of any given substance. At the absolute zero point of temperature (roughly -273°C) the entropy of any substance is zero. When you bring the substance into any other state by slow, reversible little steps (even if thereby the substance changes its physical or chemical nature or splits up into two or more parts be of different physical or chemical nature) the entropy increases by an amount which is computed by dividing every little portion of heat you had to supply in that procedure by the absolute temperature at which it was supplied – and by summing up all these small contributions. To give an example, when you melt a solid, its entropy increases by the amount of the heat of fusion divided by the temperature at the melting-point. You see from this, that the unit in which entropy is measured is cal./C (just as the calorie is the unit of heat or the centimetre the unit of length).
The Statistical Meaning of Entropy
I have mentioned this technical definition simply in order to remove entropy from the atmosphere of hazy mystery that frequently veils it. Much more important for us here is the bearing on the statistical concept of order and disorder, a connection that was revealed by the investigations of Boltzmann and Gibbs in statistical physics. This too is an exact quantitative connection, and is expressed by
entropy = k logD,
where k is the so-called Boltzmann constant ( = $3.2983 . 10^{-24}$ cal./C), and D a quantitative measure of the atomistic disorder of the body in question. To give an exact explanation of this quantity D in brief non-technical terms is well-nigh impossible. The disorder it indicates is partly that of heat motion, partly that which consists in different kinds of atoms or molecules being mixed at random, instead of being neatly separated, e.g. the sugar and water molecules in the example quoted above. Boltzmann’s equation is well illustrated by that example. The gradual ‘spreading out’ of the sugar over all the water available increases the disorder D, and hence (since the logarithm of D increases with D) the entropy. It is also pretty clear that any supply of heat increases the turmoil of heat motion, that is to say, increases D and thus increases the entropy; it is particularly clear that this should be so when you melt a crystal, since you thereby destroy the neat and permanent arrangement of the atoms or molecules and turn the crystal lattice into a continually changing random distribution.
An isolated system or a system in a uniform environment (which for the present consideration we do best to include as the part of the system we contemplate) increases its entropy and more or less rapidly approaches the inert state of maximum entropy. We now recognize this fundamental law of physics to be just the natural tendency of things to approach the chaotic state (the same tendency that the books of a library or the piles of papers and manuscripts on a writing desk display) unless we obviate it. (The analogue of irregular heat motion, in this case, is our handling those objects now and again to without troubling to put them back in their proper places.)
Organization Maintained by Extracting ‘Order’ from the Environment
How would we express in terms of the statistical theory the marvellous faculty of a living organism, by which it delays the decay into thermodynamical equilibrium (death)? We said before: ‘It feeds upon negative entropy’, attracting, as it were, a stream of negative entropy upon itself, to compensate the entropy increase it produces by living and thus to maintain itself on a stationary and fairly low entropy level.
If D is a measure of disorder, its reciprocal, 1/D, can be regarded as a direct measure of order. Since the logarithm of 1/D is just minus the logarithm of D, we can write Boltzmann’s equation thus:
-(entropy) = k log (1/D).
Hence the awkward expression ‘negative entropy’ can be replaced by a better one: entropy, taken with the negative sign, is itself a measure of order. Thus the device by which an organism maintains itself stationary at a fairly high level of orderliness ( = fairly low level of entropy) really consists continually sucking orderliness from its environment. This conclusion is less paradoxical than it appears at first sight. Rather could it be blamed for triviality. Indeed, in the case of higher animals we know the kind of orderliness they feed upon well enough, viz. the extremely well-ordered state of matter in more or less complicated organic compounds, which serve them as foodstuffs. After utilizing it they return it in a very much degraded form – not entirely degraded, however, for plants can still make use of it. (These, of course, have their most powerful supply of ‘negative entropy’, the sunlight)
Note to Chapter 6
The remarks on negative entropy have met with doubt and opposition from physicist colleagues. Let me say first, that if I had been catering for them alone I should have let the discussion turn on free energy instead. It is the more familiar notion in this context. But this highly technical term seemed linguistically too near to energy for making the average reader alive to the contrast between the two things. He is likely to take free as more or less an epitheton ornans without much relevance, while actually the concept is a rather intricate one, whose relation to Boltzmann’s order-disorder principle is less easy to trace than for entropy and ‘entropy taken with a negative sign’, which by the way is not my invention. It happens to be precisely the thing on which Boltzmann’s original argument turned.
But F. Simon has very pertinently pointed out to me that my simple thermodynamical considerations cannot account for our having to feed on matter ‘in the extremely well ordered state of more or less complicated organic compounds’ rather than on charcoal or diamond pulp. He is right. But to the lay reader I must explain that a piece of un-burnt coal or diamond, together with the amount of oxygen needed for its combustion, is also in an extremely well ordered state, as the physicist understands it. Witness to this: if you allow the reaction, the burning of the coal, to take place, a great amount of heat is produced. By giving it off to the surroundings, the system disposes of the very considerable entropy increase entailed by the reaction, and reaches a state in which it has, in point of fact, roughly the same entropy as before.
Yet we could not feed on the carbon dioxide that results from the reaction. And so Simon is quite right in pointing out to me, as he did, that actually the energy content of our food does matter; so my mocking at the menu cards that indicate it was out of place. Energy is needed to replace not only the mechanical energy of our bodily exertions, but also the heat we continually give off to the environment. And that we give off heat is not accidental, but essential. For this is precisely the manner in which we dispose of the surplus entropy we continually produce in our physical life process.
This seems to suggest that the higher temperature of the warm-blooded animal includes the advantage of enabling it to get rid of its entropy at a quicker rate, so that it can afford a more intense life process. I am not sure how much truth there is in this argument (for which I am responsible, not Simon). One may hold against it, that on the other hand many warm-blooders are protected against the rapid loss of heat by coats of fur or feathers. So the parallelism between body temperature and ‘intensity of life’, which I believe to exist, may have to be accounted for more directly by van’t Hoff’s law, mentioned on p. 65: the higher temperature itself speeds up the chemical reactions involved in living. (That it actually does, has been confirmed experimentally in species which take the temperature of the surroundings.).
Chapter 7: Is Life Based on the Laws of Physics?
New Laws to be Expected in the Organism
What I wish to make clear in this last chapter is, in short, that from all we have learnt about the structure of living matter, we must be prepared to find it working in a manner that cannot be reduced to the ordinary laws of physics. And that not on the ground that there is any ‘new force’ or what not, directing the behaviour of the single atoms within a living organism, but because the construction is different from a anything we have yet tested in the physical laboratory. To put it crudely, an engineer, familiar with heat engines only, will, after inspecting the construction of an electric motor, be prepared to find it working along principles which he does not yet understand. He finds the copper familiar to him in kettles used here in the form of long, wires wound in coils; the iron familiar to him in levers and bars and steam cylinders here filling the interior of those coils of copper wire. He will be convinced that it is the same copper and the same iron, subject to the same laws of Nature, and he is right in that. The difference in construction is enough to prepare him for an entirely different way of functioning. He will not suspect that an electric motor is driven by a ghost because it is set spinning by the turn of a switch, without boiler and steam.
Reviewing the Biological Situation
The unfolding of events in the life cycle of an organism exhibits an admirable regularity and orderliness, unrivalled by anything we meet with in inanimate matter. We find it controlled by a supremely well-ordered group of atoms, which represent only a very small fraction of the sum total in every cell. Moreover, from the view we have formed of the mechanism of mutation we conclude that the dislocation of just a few atoms within the group of ‘governing atoms’ of the germ cell suffices to bring about a well-defined change in the large-scale hereditary characteristics of the organism.
These facts are easily the most interesting that science has revealed in our day. We may be inclined to find them, after all, not wholly unacceptable. An organism’s astonishing gift of concentrating a ‘stream of order’ on itself and thus escaping that the decay into atomic chaos – of ‘drinking orderliness’ from a suitable environment – seems to be connected with the presence of the ‘aperiodic solids’, the chromosome molecules, which doubtless represent the highest degree of well-ordered atomic association we know of – much higher than the ordinary periodic crystal – in virtue of the individual role every atom and every radical is playing here.
To put it briefly, we witness the event that existing order displays the power of maintaining itself and of producing orderly events. That sounds plausible enough, though in finding it plausible we, no doubt, draw on experience concerning social organization and other events which involve the activity of organisms. And so it might seem that something like a vicious circle is implied.
Summarizing the Physical Situation
However that may be, the point to emphasize again and again is that to the physicist the state of affairs is not only not plausible but most exciting, because it is unprecedented. Contrary to the common belief, the regular course of events, governed by the laws of physics, is never the consequence of one well-ordered configuration of atoms – not unless that configuration of atoms repeats itself a great number of times, either as in the periodic crystal or as in a liquid or in a gas composed of a great number of identical molecules.
Even when the chemist handles a very complicated molecule in vitro he is always faced with an enormous number of like molecules. To them his laws apply. He might tell you, for example, that one minute after he has started some particular reaction half of the molecules will have reacted, and after a second minute three-quarters of them will have done so. But whether any particular molecule, supposing you could follow its course, will be among those which have reacted or among those which are still untouched, he could not predict. That is a matter of pure chance.
This is not a purely theoretical conjecture. It is not that we can never observe the fate of a single small group of atoms or even of a single atom. We can, occasionally. But whenever we do, we find complete irregularity, co-operating to produce regularity only on the average. We have dealt with an example in chapter 1. The Brownian movement of a small particle suspended in a liquid is completely irregular. But if there are many similar particles, they will by their irregular movement give rise to the regular phenomenon of diffusion. The disintegration of a single radioactive atom is observable (it emits a projectile which causes a visible scintillation on a fluorescent screen). But if you are given a single radioactive atom, its probable lifetime is much less certain than that of a healthy sparrow. Indeed, nothing more can be said about it than this: as long as it lives (and that may be for thousands of years) the chance of its blowing up within the next second, whether large or small, remains the same. This patent lack of individual determination nevertheless results in the exact exponential law of decay of a large number of radioactive atoms of the same kind.
The Striking Contrast
In biology we are faced with an entirely different situation. A single group of atoms existing only in one copy produces orderly events, marvellously tuned in with each other and with the environment according to most subtle laws. I said existing only in one copy, for after all we have the example of the egg and of the unicellular organism. In the following stages of a higher organism the copies are multiplied, that is true. But to what extent? Something like $10^{14}$ in a grown mammal, I understand. What is that! Only a millionth of the number of molecules in one cubic inch of air. Though comparatively bulky, by coalescing they would form but a tiny drop of liquid. And look at the way they are actually distributed. Every cell harbours just one of them (or two, if we bear in mind diploidy). Since we know the power this tiny central office has in the isolated cell, do they not resemble stations of local government dispersed through the body, communicating with each other with great ease, thanks to the code that is common to all of them?
Well, this is a fantastic description, perhaps less becoming a scientist than a poet. However, it needs no poetical imagination but only clear and sober scientific reflection to recognize that we are here obviously faced with events whose regular and lawful unfolding is guided by a ‘mechanism’ entirely different from the ‘probability mechanism’ of physics. For it is simply a fact of observation that the guiding principle in every cell is embodied in a single atomic association existing only one copy (or sometimes two) – and a fact of observation that it results in producing events which are a paragon of orderliness. Whether we find it astonishing or whether we find it quite plausible that a small but highly organized group of atoms be capable of acting in this manner, the situation is unprecedented, it is unknown anywhere else except in living matter. The physicist and the chemist, investigating inanimate matter, have never witnessed phenomena which they had to interpret in this way. The case did not arise and so our theory does not cover it – our beautiful statistical theory of which we were so justly proud because it allowed us to look behind the curtain, to watch the magnificent order of exact physical law coming forth from atomic and molecular disorder; because it revealed that the most important, the most general, the all-embracing law of entropy could be understood without a special assumption ad hoc, for it is nothing but molecular disorder itself.
Two Ways of Producing Orderliness
The orderliness encountered in the unfolding of life springs from a different source. It appears that there are two different ‘mechanisms’ by which orderly events can be produced: the ‘statistical mechanism’ which produces ‘order from disorder’ and the new one, producing ‘order from order’. To the unprejudiced mind the second principle appears to be much simpler, much more plausible. No doubt it is. That is why physicists were so proud to have fallen in with the other one, the ‘order-from-disorder’ principle, which is actually followed in Nature and which alone conveys an understanding of the great line of natural events, in the first place of their irreversibility. But we cannot expect that the ‘laws of physics’ derived from it suffice straightaway to explain the behaviour of living matter, whose most striking features are visibly based to a large extent on the ‘order-from-order’ principle. You would not expect two entirely different mechanisms to bring about the same type of law – you would not expect your latch-key, to open your neighbour’s door as well.
We must therefore not be discouraged by the difficulty of interpreting life by the ordinary laws of physics. For that is just what is to be expected from the knowledge we have gained of the structure of living matter. We must be prepared to find a new type of physical law prevailing in it. Or are we to term it a non-physical, not to say a super-physical, law?
The New Principle is Not Alien to Physics
No. I do not think that. For the new principle that is involved is a genuinely physical one: it is, in my opinion, nothing else than the principle of quantum theory over again. To explain this, we have to go to some length, including a refinement, not to say an amendment, of the assertion previously made, namely, that all physical laws are based on statistics. This assertion, made again and again, could not fail to arouse contradiction. For, indeed, there are phenomena whose conspicuous features are visibly based directly on the ‘order-from-order’ principle and appear to have nothing to do with statistics or molecular disorder.
The order of the solar system, the motion of the planets, is maintained for an almost indefinite time. The constellation of this moment is directly connected with the constellation at any particular moment in the times of the Pyramids; it can be traced back to it, or vice versa. Historical eclipses have been calculated and have been found in close agreement with historical records or have even in some cases served to correct the accepted chronology. These calculations do not imply any statistics, they are based solely on Newton’s law of universal attraction.
Nor does the regular motion of a good clock or any similar mechanism appear to have anything to do with statistics. In short, all purely mechanical events seem to follow distinctly and directly the ‘order-from-order’ principle. And if we say ‘mechanical’, the term must be taken in a wide sense. A very useful kind of clock is, as you know, based on the regular transmission of electric pulses from the power station.
I remember an interesting little paper by Max Planck on the topic ‘The Dynamical and the Statistical Type of Law’ (‘Dynamische und Statistische Gesetzmassigkeit’). The distinction is precisely the one we have here labelled as ‘order from order’ and ‘order from disorder’. The object of that paper was to show how the interesting statistical type of law, controlling large-scale events, is constituted from the dynamical laws supposed to govern the small-scale events, the interaction of the single atoms and molecules. The latter type is illustrated by large-scale mechanical phenomena, as the motion of the planets or of a clock, etc.
Thus it would appear that the ‘new’ principle, the order-from-order principle, to which we have pointed with great solemnity as being the real clue to the understanding of life, is not at all new to physics. Planck’s attitude even vindicates priority for it. We seem to arrive at the ridiculous conclusion that the clue to the understanding of life is that it is based on a pure mechanism, a ‘clock-work’ in the sense of Planck’s paper. The conclusion is not ridiculous and is, in my opinion, not entirely wrong, but it has to be taken ‘with a very big grain of salt’.
The Motion of a Clock
Let us analyse the motion of a real clock accurately. It is not at all a purely mechanical phenomenon. A purely mechanical clock would need no spring, no winding. Once set in motion, it would go on forever. A real clock without a spring stops after a few beats of the pendulum, its mechanical energy is turned into heat. This is an infinitely complicated atomistic process. The general picture the physicist forms of it compels him to admit that the inverse process is not entirely impossible: a springless clock might suddenly begin to move, at the expense of the heat energy of its own cog wheels and of the environment. The physicist would have to say: The clock experiences an exceptionally intense fit of Brownian movement. We have seen in chapter 2 (p. 16) that with a very sensitive torsional balance (electrometer or galvanometer) that sort of thing happens all the time. In the case of a clock it is, of course, infinitely unlikely.
Whether the motion of a clock is to be assigned to the dynamical or to the statistical type of lawful events (to use Planck’s expressions) depends on our attitude. In calling it a dynamical phenomenon we fix attention on the regular going that can be secured by a comparatively weak spring, which overcomes the small disturbances by heat motion, so that we may disregard them. But if we remember that without a spring the clock is gradually slowed down by friction, we find that this process can only be understood as a statistical phenomenon.
However insignificant the frictional and heating effects in a clock may be from the practical point of view, there can be no doubt that the second attitude, which does not neglect them, is the more fundamental one, even when we are faced with the regular motion of a clock that is driven by a spring. For it must not be believed that the driving mechanism really does away with the statistical nature of the process. The true physical picture includes the possibility that even a regularly going clock should all at once invert its motion and, working backward, rewind its own spring – at the expense of the heat of the environment. The event is just a little less likely than a ‘Brownian fit’ of a clock without driving mechanism.
Clockwork After All Statistical
Let us now review the situation. The ‘simple’ case we have analysed is representative of many others – in fact of all such appear to evade the all-embracing principle of molecular statistics. Clockworks made of real physical matter (in contrast to imagination) are not true ‘clock-works’. The element of chance may be more or less reduced, the likelihood of the clock suddenly going altogether wrong may be infinitesimal, but it always remains in the background. Even in the motion of the celestial bodies irreversible frictional and thermal torsional influences are not wanting. Thus the rotation of the earth is slowly diminished by tidal friction, and along with this of course, reduction the moon gradually recedes from the earth, which would not happen if the earth were a completely rigid rotating sphere.
Nevertheless the fact remains that ‘physical clock-works’ visibly display very prominent ‘order-from-order’ features – the type that aroused the physicist’s excitement when he encountered them in the organism. It seems likely that the two cases have after all something in common. It remains to be seen what this is and what is the striking difference which makes case of the organism after all novel and unprecedented.
Nernst’s Theorem
When does a physical system – any kind of association atoms – display ‘dynamical law’ (in Planck’s meaning) ‘clock-work features’? Quantum theory has a very short answer to this question, viz. at the absolute zero of temperature. As zero temperature is approached the molecular disorder ceases to have any bearing on physical events. This fact was, by the way, not discovered by theory, but by carefully investigating chemical reactions over a wide range of temperatures and extrapolating the results to zero temperature – which cannot actually be reached. This is Walther Nernst’s famous ‘Heat Theorem’, which is sometimes, and not unduly, given the proud name of the ‘Third Law of Thermodynamics’ (the first being the energy principle, the second the entropy principle).
Quantum theory provides the rational foundation of Nernst’s empirical law, and also enables us to estimate how closely a system must approach to the absolute zero in order to display an approximately ‘dynamical’ behaviour. What temperature is in any particular case already practically equivalent to zero?
Now you must not believe that this always has to be a very low temperature. Indeed, Nernst’s discovery was induced by the fact that even at room temperature entropy plays a astonishingly insignificant role in many chemical reactions (Let me recall that entropy is a direct measure of molecular disorder, viz. its logarithm.).
The Pendulum Clock is Virtually at Zero Temperature
What about a pendulum clock? For a pendulum clock room temperature is practically equivalent to zero. That is the reason why it works ‘dynamically’. It will continue to work as it does if you cool it (provided that you have removed all traces of oil!). But it does not continue to work if you heat it above room temperature, for it will eventually melt.
The Relation Between Clockwork and Organism
That seems very trivial but it does, I think, hit the cardinal point. Clockworks are capable of functioning ‘dynamically’, because they are built of solids, which are kept in shape by London-Heitler forces, strong enough to elude the disorderly tendency of heat motion at ordinary temperature.
Now, I think, few words more are needed to disclose the point of resemblance between a clockwork and an organism. It is simply and solely that the latter also hinges upon a solid – the aperiodic crystal forming the hereditary substance, largely withdrawn from the disorder of heat motion. But please do not accuse me of calling the chromosome fibres just the ‘cogs of the organic machine’ – at least not without a reference to the profound physical theories on which the simile is based.
For, indeed, it needs still less rhetoric to recall the fundamental difference between the two and to justify the epithets novel and unprecedented in the biological case. The most striking features are: first, the curious distribution of the cogs in a many-celled organism, for which I may refer to a very the somewhat poetical description on p. 79; and secondly, the fact that the single cog is not of coarse human make, but is the finest masterpiece ever achieved along the lines of the Lord’s quantum mechanics.
Epilogue: On Determinism and Free Will
As a reward for the serious trouble I have taken to expound the purely scientific aspects of our problem sine ira et studio, I beg leave to add my own, necessarily subjective, view of the philosophical implications.
According to the evidence put forward in the preceding pages the space-time events in the body of a living being which correspond to the activity of its mind, to its self conscious or any other actions, are (considering also their complex structure and the accepted statistical explanation of physico-chemistry) if not strictly deterministic at any rate statistico-deterministic. To the physicist I wish to emphasize that in my opinion, and contrary to the opinion upheld in some quarters, quantum indeterminacy plays no biologically relevant role in them, except perhaps by enhancing their purely accidental character in such events as meiosis, natural and X-ray-induced mutation and so on – and this is in any case obvious and well recognized.
For the sake of argument, let me regard this as a fact, as I believe every unbiased biologist would, if there were not the well-known, unpleasant feeling about ‘declaring oneself to be a pure mechanism’. For it is deemed to contradict Free Will as warranted by direct introspection.
But immediate experiences in themselves, however various and disparate they be, are logically incapable of contradicting each other. So let us see whether we cannot draw the correct, non-contradictory conclusion from the following two premises:
- My body functions as a pure mechanism according to the Laws of Nature.
- Yet I know, by incontrovertible direct experience, that I am directing its motions, of which I foresee the effects, that may be fateful and all-important, in which case I feel and take full responsibility for them.
The only possible inference from these two facts is, I think, that I – I in the widest meaning of the word, that is to say, every conscious mind that has ever said or felt ‘I’ – am the person, if any, who controls the ‘motion of the atoms’ according to the Laws of Nature.
Within a cultural milieu (Kulturkreis) where certain conceptions (which once had or still have a wider meaning amongst other peoples) have been limited and specialized, it is daring to give to this conclusion the simple wording that it requires. In Christian terminology to say: ‘Hence I am God Almighty’ sounds both blasphemous and lunatic. But please disregard these connotations for the moment and consider whether the above inference is not the closest a biologist can get to proving God and immortality at one stroke.
In itself, the insight is not new. The earliest records to my knowledge date back some 2,500 years or more. From the early great Upanishads the recognition Athman = Brahman (the personal self equals the omnipresent, all-comprehending eternal self) was in Indian thought considered, far from being blasphemous, to represent the quintessence of deepest insight into the happenings of the world. The striving of all the scholars of Vedanta was, after having learnt to pronounce with their lips, really to assimilate in their minds this grandest of all thoughts.
Again, the mystics of many centuries, independently, yet in perfect harmony with each other (somewhat like the particles in an ideal gas) have described, each of them, the unique experience of his or her life in terms that can be condensed in the phrase: Deus Factus Sum (I have become God).
To Western ideology the thought has remained a stranger, in spite of Schopenhauer and others who stood for it and in spite of those true lovers who, as they look into each other’s eyes, become aware that their thought and their joy are numerically one – not merely similar or identical; but they, as a rule, are emotionally too busy to indulge in clear thinking, in which respect they very much resemble the mystic.
Allow me a few further comments. Consciousness is never experienced in the plural, only in the singular. Even in the pathological cases of split consciousness or double personality the two persons alternate, they are never manifest simultaneously. In a dream we do perform several characters at the same time, but not indiscriminately: we are one of them; in him we act and speak directly, while we often eagerly await answer or response of another person, unaware of the fact that it is we who control his movements and his speech just as much as our own.
How does the idea of plurality (so emphatically opposed by the Upanishad writers) arise at all? Consciousness finds itself intimately connected with, and dependent on, the physical state of a limited region of matter, the body. (Consider the changes of mind during the development of the body, at puberty, ageing, dotage, etc., or consider the effects of fever, intoxication, narcosis, lesion of the brain and so on.) Now there is a great plurality of similar bodies. Hence the pluralization of consciousnesses or minds seems a very suggestive hypothesis. Probably all simple, ingenuous people, as well as the great majority of Western philosophers, have accepted it.
It leads almost immediately to the invention of souls, as many as there are bodies, and to the question whether they are mortal as the body is or whether they are immortal and capable of existing by themselves. The former alternative is distasteful while the latter frankly forgets, ignores or disowns the fact upon which the plurality hypothesis rests. Much sillier questions have been asked: Do animals also have souls? It has even been questioned whether women, or only men, have souls.
Such consequences, even if only tentative, must make us suspicious of the plurality hypothesis, which is common to all official Western creeds. Are we not inclining to much greater nonsense, if in discarding their gross superstitions we retain their naive idea of plurality of souls, but ‘remedy’ it by declaring the souls to be perishable, to be annihilated with the respective bodies?
The only possible alternative is simply to keep to the immediate experience that consciousness is a singular of which the plural is unknown; that there is only one thing and that what seems to be a plurality is merely a series of different personality aspects of this one thing, produced by a deception (the Indian Maja); the same illusion is produced in a gallery of mirrors, and in the same way Gaurisankar and Mt Everest turned out to be the same peak seen from different valleys.
There are, of course, elaborate ghost-stories fixed in our minds to hamper our acceptance of such simple recognition. E.g. it has been said that there is a tree there outside my window but I do not really see the tree. By some cunning device of which only the initial, relatively simple steps are explored, the real tree throws an image of itself into my consciousness, and that is what I perceive. If you stand by my side and look at the same tree, the latter manages to throw an image into your soul as well. I see my tree and you see yours (remarkably like mine), and what the tree in itself is we do not know. For this extravagance Kant is responsible. In the order of ideas which regards consciousness as a singulare tantum it is conveniently replaced by the statement that there is obviously only one tree and all the image business is a ghost-story.
Yet each of us has the indisputable impression that the sum total of his own experience and memory forms a unit, quite distinct from that of any other person. He refers to it as ‘I’ and What is this ‘I’?
If you analyse it closely you will, I think, find that it is just a little more than a collection of single data (experiences and memories), namely the canvas upon which they are collected. And you will, on close introspection, find that what you really mean by ‘I’ is that ground-stuff upon which they are collected. You may come to a distant country, lose sight of all your friends, may all but forget them; you acquire new friends, you share life with them as intensely as you ever did with your old ones. Less and less important will become the fact that, while living your new life, you still recollect the old one. ‘The youth that was I’, you may come to speak of him in the third person, indeed the protagonist of the novel you are reading is probably nearer to your heart, certainly more intensely alive and better known to you. Yet there has been no intermediate break, no death. And even if a skilled hypnotist succeeded in blotting out entirely all your earlier reminiscences, you would not find that he had killed you. In no case is there a loss of personal existence to deplore.
Nor will there ever be.
Note to the Epilogue
The point of view taken here levels with what Aldous Huxley has recently – and very appropriately – called The Perennial Philosophy. His beautiful book (London, Chatto and Windus, 1946) is singularly fit to explain not only the state of affairs, but also why it is so difficult to grasp and so liable to meet with opposition.