Intermediate Representations in Compilers: Static Single Assignment (SSA)

Compilers are program translators – they translate program from one language to another while preserving the semantics. Usually the source language is higher level programming language like C++ or Java and the target language is machine level language like assembly or virtual machine language like JVM. Although it doesn’t have to be like this, target language is almost always at lower level than the source language.

To do such a transformation, it helps to have what are called intermediate representations or IRs of the program. Instead of translating in one single go to the target language, translation happens progressively between these representations. This process is also called lowering because we’re converting from higher level representations to progressively lower level representations. Some recognizable intermediate representations for imperative languages include abstract syntax tree, control flow graph and static single assignment (SSA) form. For lisp-like/functional languages, continuation passing style (CPS) is a popular intermediate representation.

In this series of posts, we’ll explain how SSA and CPS representations work. We will then show how these are pretty much the same representations. This series is inspired by Delphine Demange’s PhD thesis on semantics of intermediate representations.

Static Single Assignment (SSA) Form

Static single assignment (SSA) is one of the most popular intermediate representations out there. Stalwarts of compiler toolchains, both GCC and LLVM, use this form as IR for multiple languages. SSA introduces the restriction that each variable is assigned only once and never change the values. If a variable is modified in the original program, a new variable is introduced instead of modifying the old one. This IR is designed to be easily optimizable and neutral between source languages. To give you an idea, here’s how SSA for GCD program looks like:

We will use LLVM IR to illustrate the SSA form. In the process, we should be able to learn how LLVM is generated for different constructs!

Functions

Let’s examine LLVM IR for the following simple C program:

// ssa.c
int fun(int x, int y){
    return x + y;
}

To compile this to LLVM IR, you can run the following command: clang -S -emit-llvm -O3 ssa.c. I’ll simplify this representation manually to make it easy to understand.

; ssa.ll
; function definition
define i32 @fun(i32 %x, i32 %y) {
    ; temporary variable is created
    ; addtmp = x + y
    %addtmp = add i32 %x, %y
    ; and that is returned
    ret i32 %addtmp
}

LLVM IR is typed: that’s the reason why we have i32 next to instruction add to indicate we’re operating on 32 bit integers. To run this LLVM code, let’s create a simple runtime function:

// run.c
#include <stdio.h>

extern int fun(int, int);

int main(){
    printf("result: %d\n", fun(7, 11));
}

Compile everything together and run resulting executable:

$ clang ssa.ll run.c
$ ./a.out
result: 18

Variable Modification

That was straight forward. Let’s see how LLVM IR for this function will look like:

//ssa.c
int fun(int x, int y){
    x = (x * 5) / 3;
    y = y + 10;
    return x + y;
}

In this function, x and y are being modified. So we’ll need to create temporary variables to hold modified values. The C program above will get transformed to something like this:

; ssa.ll
define i32 @fun(i32 %x, i32 %y) {
    ; x1 = x * 5
    %x1 = mul nsw i32 %x, 5
    ; x2 = x1 / 3
    %x2 = sdiv i32 %x1, 3
    ; y1 = y + 10
    %y1 = add i32 %y, 10
    ; addtmp = x2 + y1
    %addtmp = add nsw i32 %x2, %y1
    ret i32 %addtmp
}

Compile and verify that we get expected result:

$ clang ssa.ll run.c
$ ./a.out
result: 32

If you were to do something like this, where x is modified:

; ssa.ll
define i32 @fun(i32 %x, i32 %y) {
    ; this is an error
    %x = mul nsw i32 %x, 5
    %addtmp = add nsw i32 %x, %y
    ret i32 %addtmp
}

You’ll get an error:

$ clang ssa.ll run.c
ssa.ll:4:5: error: multiple definition of local value named 'x'
    %x = mul nsw i32 %x, 5
    ^
1 error generated.

Conditionals

What happens if there’s a conditional block? Following a conditional, a variable could have either value. To indicate that final value is one of the above, we use something called as phi function. Consider the following function:

//ssa.c
int fun(int x, int y){
    int z;
    if (x > 1) {
        z = x + y;
    }
    else if (x < -1) {
        z = - x + y;
    } else {
        z = x - y;
    }
    return z;
}

Its LLVM IR will look something like this:

; ssa.ll
define i32 @fun(i32 %x, i32 %y) {
    ; integer compare (icmp), signed greater than (sgt)
    ; x_gt_1 = (x > 1)
    %x_gt_1 = icmp sgt i32 %x, 1
    ; branch (br) if x_gt_1 (boolean/i1) to 'if_gt' 
    ; otherwise goto 'else'
    br i1 %x_gt_1, label %if_gt, label %else

if_gt:
    ; add = x + y
    %add = add i32 %x, %y
    ; unconditional jump to 'end'
    br label %end

else:
    ; integer compare (icmp), signed less than (slt)
    ; x_lt_neg1 = (x < -1)
    %x_lt_neg1 = icmp slt i32 %x, -1
    ; branch to 'if_lt' or 'if_else' conditional on x_lt_neg1
    br i1 %x_lt_neg1, label %if_lt, label %if_else

if_lt:
    ; sub1 = 0 - x
    %sub1 = sub i32 0, %x
    ; add1 = sub1 + y
    %add1 = add i32 %sub1, %y
    ; unconditional jump to 'end'
    br label %end

if_else:
    ; sub2 = x - y
    %sub2 = sub i32 %x, %y
    ; unconditional jump to 'end'
    br label %end

end:
    ; phi instruction: list of [variable, label]
    %z = phi i32 [ %add, %if_gt ], [ %add1, %if_lt ],
                    [ %sub2, %if_else ]
    ret i32 %z
}

Note the phi instruction in the end block that indicates that variable %z is one of %add, %add1 and %sub2 from blocks %if_gt, %if_lt and %if_else respectively

Loops

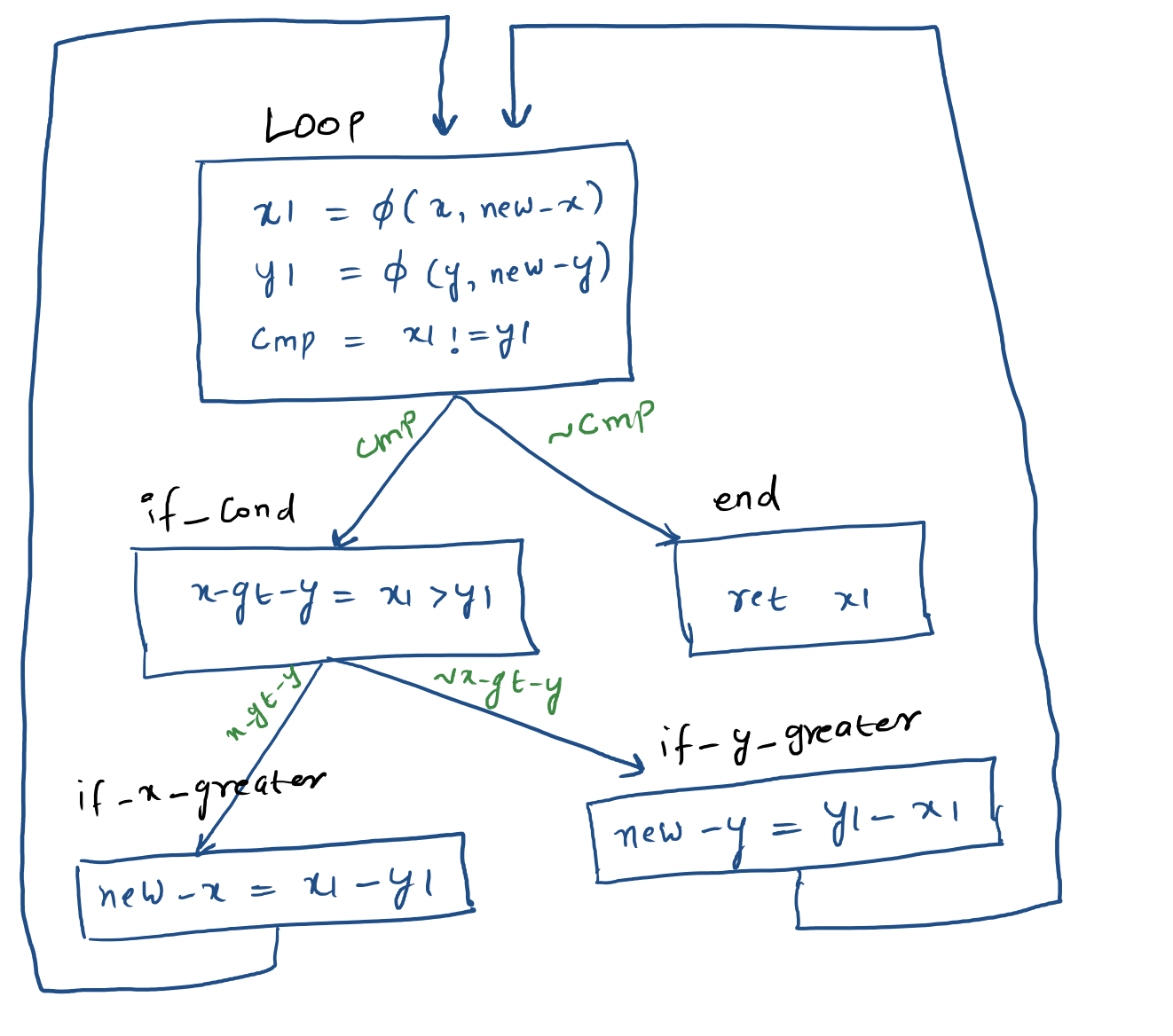
Let’s see how loops get translated in SSA. It should be not too different from conditionals because loops also use conditional branches. Here’s the function to compute GCD:

//ssa.c
int fun(int x, int y){
    while (x != y) {
        if (x > y)
            x = x - y;
        else
            y = y - x;
    }
    return x;
}

Its LLVM transformation will look something like this:

define i32 @fun(i32 %x, i32 %y) {
entry:
    br label %loop

loop:
    ; x1 = x or new_x
    %x1 = phi i32 [ %x, %entry ], [ %new_x, %if_x_greater ]
    ; y1 = y or new_y
    %y1 = phi i32 [ %y, %entry ], [ %new_y, %if_y_greater ]
    ; integer compare (icmp) not equal (ne)
    ; cmp = (x1 != y1)
    %cmp = icmp ne i32 %x1, %y1
    ; jump conditioal on %cmp to 'if_cond' or 'end' 
    br i1 %cmp, label %if_cond, label %end

if_cond:
    ; integer compare (icmp) signed greater than (sgt)
    ; x_gt_y = (x1 > y1)
    %x_gt_y = icmp sgt i32 %x1, %y1
    ; jump conditioal on %x_gt_y to 'if_x_greater' or 'if_y_greater' 
    br i1 %x_gt_y, label %if_x_greater, label %if_y_greater

if_x_greater:
    ; new_x = (x1 - y1)
    %new_x = sub i32 %x1, %y1
    ; unconditional jump to the top of loop
    br label %loop

if_y_greater:
    ; new_y = (y1 - x1)
    %new_y = sub i32 %y1, %x1
    ; unconditional jump to the top of loop
    br label %loop

end:
    ; return x1
    ret i32 %x1
}

From this it should be clear that single assignment is a static property of the program text and not the dynamic property of program execution. This should make it clear why there’s ‘static’ in the name of static single assignment form. You can see the pictorial form of this code at the top of the post.

This post should give a good taste on what SSA is and how it works. In the next post, let’s examine what continuation passing style is and how it works.

References:

1. Douglas Thain, Introduction to Compilers and Language Design
2. Delphine Demange, Semantic Foundations of Intermediate Program Representations
3. Mukul Rathi, A Complete Guide to LLVM for Programming Language Creators
4. Andrew Appel, SSA is Functional Programming