Scheme Compiler in Incremental Steps: Procedures
In this post, let us add procedures to our compiler. Procedures or functions are a basic building of any language – especially so with lisp because it was highly influenced by Alonzo Church’s lambda calculus. Lists and procedures/functions together form the basis of Lisp language.
We will use form letrec to name functions. It’s similar to let except that right hand side of bindings is a lambda. Function applications will carry keyword app like this (app f arg1 arg2). We will allow letrec only at top level to simplify things.
Therefore our language will now look like:
<program>:= <expr> | (letrec ((lvar <lambda>) ...) <expr>)
<lambda> := (lambda (var ...) <expr>)
<expr> := <immediate>
| var
| (if <expr> <expr> <expr>)
| (let ((var <expr>) ...) <expr>)
| (app lvar <expr> ...)
| (<primitive> <expr>)
Example code in our language will look like this:
(letrec ((f (lambda (x y) (+ x y)))
(g (lambda (x) (+ x 12))))
(app f 16 (app f (app g 0) (+ 1 (app g 0)))))
We will use stack to pass the arguments between caller and callee. Caller will populate the stack with arguments and set the stack base pointer rsp starting at arguments. Therefore, callee will see the truncated stack with arguments values filled near the base. Once callee is done, caller will reset the rsp to where it was. Here’s a schematic:
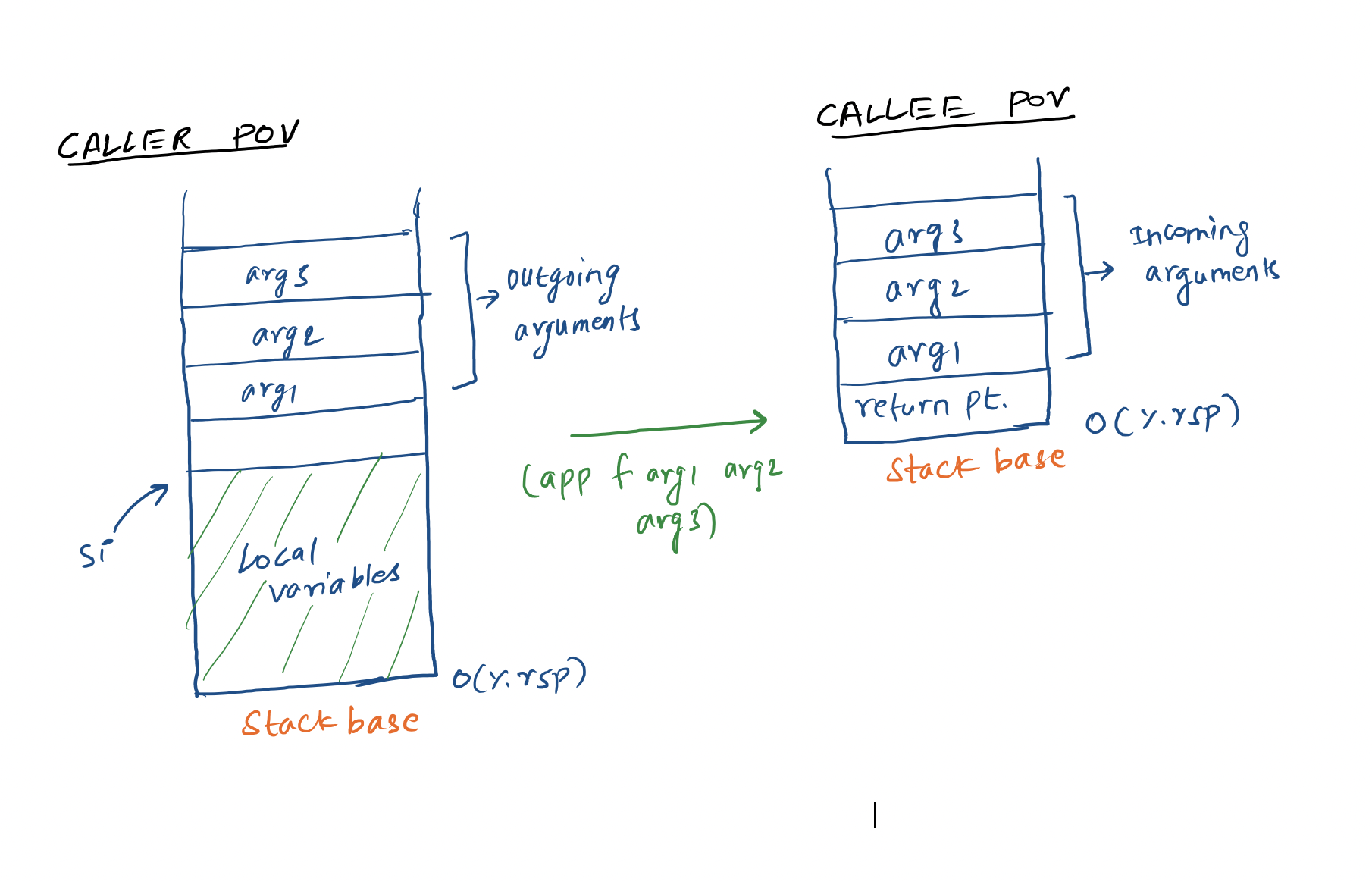
Let’s start adding three constructs letrec, lambda and app one by one.
Add letrec
This one is simple: parse the letrec form into constituents and put them into environment. Note that we’ll be adding string labels into environment to bind names to lambdas.
; in compiler.scm
(define (letrec? expr)
(and (pair? expr) (eq? (car expr) 'letrec)))
(define (letrec-bindings expr)
(cadr expr))
(define (letrec-body expr)
(caddr expr))
(define (binding-lhs b)
(car b))
(define (binding-rhs b)
(cadr b))
(define (make-letrec-env lvars labels)
; string values in env is seen as labels
(map cons lvars labels))
(define (emit-letrec expr)
(let* ((bindings (letrec-bindings expr))
(lvars (map binding-lhs bindings))
(lambdas (map binding-rhs bindings))
(labels (map (lambda (x) (unique-label)) lvars))
(env (make-letrec-env lvars labels)))
(for-each
(lambda (label expr) (emit-lambda env label expr))
labels lambdas)
(emit-scheme-entry)
(emit-expr (- word-size) env (letrec-body expr))
(emit "ret")))
Add lambda
emit-lambda emits the label that letrec has created and actual code of the procedure. We call argument names of lambda as ‘formals’ or fmls in below code. Note that we extend the environment of lambda by binding formals to the stack. This is because we expect caller to put the actual argument values in the stack.
; in compiler.scm
(define (lambda-fmls expr)
(cadr expr))
(define (lambda-body expr)
(caddr expr))
(define (process-lambda si env fmls body)
; recursively process formals
(cond
((null? fmls)
(emit-expr si env body))
(else
(process-lambda
(next-stack-index si)
; we expect formal values to be in stack
(extend-env (car fmls) si env)
(cdr fmls)
body))))
(define (emit-lambda env label expr)
(emit "~a:" label)
(process-lambda (- word-size) env
(lambda-fmls expr) (lambda-body expr))
(emit "ret"))
Add app
By now we have emitted code for procedures and put the names of the procedures in our environment. Now we need to implement calling of these procedures. We will utilize instruction call which does the following:
- Compute address of instruction after the call instruction i.e. return point
- Decrement
%rspby 8 - Saves the return point at
0(%rsp) - Directs the execution to label
ret inside the label will do the following:
- Load return address from
0(%rsp) - Increment the value by 8
- Directs the execution to return point
Therefore, we have to leave base of the stack empty for storing return address. Thus the empty cell in above figure. We fill rest of the stack with the values of caller arguments.
; in compiler.scm
(define (app? expr)
(and (pair? expr) (eq? (car expr) 'app)))
(define (app-args expr)
(cddr expr))
(define (app-target expr)
(cadr expr))
(define (emit-arguments si env args)
; fill stack with arg values
(unless (null? args)
(emit-expr si env (car args))
(emit-stack-save si)
(emit-arguments (- si word-size) env (cdr args))))
(define (emit-adjust-base diff)
(emit "add $~a, %rsp" diff))
(define (app-label lvar env)
(cond
((and (assoc lvar env) (string? (cdr (assoc lvar env))))
(cdr (assoc lvar env)))
(else (error "unknown procedure: " lvar))))
(define (emit-app si env expr)
; leave base of call stack for saving return address
(emit-arguments (- si word-size) env (app-args expr))
; change stack pointer to pass arguments
(emit-adjust-base (+ si word-size))
; call label for the lambda
(emit "call ~a" (app-label (app-target expr) env))
; reset stack after call to where it was before
(emit-adjust-base (- (+ si word-size))))
Putting it All Together
Let’s put all these together at top-level compile-program
; in compiler.scm
(define (emit-scheme-entry)
(emit "L_scheme_entry:"))
(define (compile-program x)
(if (letrec? x)
(emit-letrec x)
(begin
(emit-scheme-entry)
; initialize stack index (- word-size) so as
; not to overwrite return address
(emit-expr (- word-size) '() x)
(emit "ret"))))
(define (emit-expr si env expr)
(cond
((immediate? expr) (emit-immediate expr))
((variable? expr) (emit-variable-ref env expr))
((let? expr) (emit-let si env expr))
((if? expr) (emit-if si env expr))
((primcall? expr) (emit-primcall si env expr))
((app? expr) (emit-app si env expr))
(else (error "syntax error: " expr))))
Since we’re emitting L_scheme_entry in compiler.scm, we should remove that line in linker.scm:
; edit in linker.scm
(define (build x)
(define output-file (open-output-file "/tmp/scheme_entry.s"))
(output-file-param output-file)
(display (string-append
".text\n"
".p2align 4\n"
".globl scheme_entry\n"
".type scheme_entry, @function\n"
"scheme_entry:\n"
"mov %rsp, %rcx\n"
"mov %rdi, %rsp\n"
"call L_scheme_entry\n"
"mov %rcx, %rsp\n"
"ret\n")
output-file)
(compile-program x)
(display (string-append
".LFE0:\n"
".size scheme_entry, .-scheme_entry\n"
".section .note.GNU-stack,\"\",@progbits\n")
output-file)
(close-output-port output-file))
Finally add tests
; add in tests.scm
; procedures
(run-test '(letrec () 12) "12\n")
(run-test '(letrec () (let ((x 5)) (+ x x))) "10\n")
(run-test '(letrec ((f (lambda () 5))) 7) "7\n")
(run-test '(letrec ((f (lambda () 5)))
(let ((x 12)) x)) "12\n")
(run-test '(letrec ((f (lambda () 5)))
(app f)) "5\n")
(run-test '(letrec ((f (lambda () 5)))
(let ((x (app f))) x)) "5\n")
(run-test '(letrec ((f (lambda () 5)))
(+ (app f) 6)) "11\n")
(run-test '(letrec ((f (lambda () 5)))
(- 20 (app f))) "15\n")
(run-test '(letrec ((f (lambda () 5)))
(+ (app f) (app f))) "10\n")
(run-test '(letrec ((f (lambda () (+ 5 7)))
(g (lambda () 13)))
(+ (app f) (app g))) "25\n")
(run-test '(letrec ((f (lambda (x) (+ x 12))))
(app f 13)) "25\n")
(run-test '(letrec ((f (lambda (x) (+ x 12))))
(app f (app f 10))) "34\n")
(run-test '(letrec ((f (lambda (x) (+ x 12))))
(app f (app f (app f 0)))) "36\n")
(run-test '(letrec ((f (lambda (x y) (+ x y)))
(g (lambda (x) (+ x 12))))
(app f 16
(app f (app g 0)
(+ 1 (app g 0))))) "41\n")
(run-test '(letrec ((f (lambda (x) (app g x x)))
(g (lambda (x y) (+ x y))))
(app f 12)) "24\n")
(run-test '(letrec ((f (lambda (x)
(if (zero? x)
1
(* x (app f (sub1 x)))))))
(app f 5)) "120\n")
(run-test '(letrec ((e (lambda (x)
(if (zero? x) #t (app o (sub1 x)))))
(o (lambda (x)
(if (zero? x) #f (app e (sub1 x))))))
(app e 25)) "#f\n")
And verify everything works.
$ guile tests.scm
...
(letrec ((f (lambda (x) (+ x 12)))) (app f (app f (app f 0)))): passed
(letrec ((f (lambda (x y) (+ x y))) (g (lambda (x) (+ x 12)))) (app f 16 (app f (app g 0) (+ 1 (app g 0))))): passed
(letrec ((f (lambda (x) (app g x x))) (g (lambda (x y) (+ x y)))) (app f 12)): passed
(letrec ((f (lambda (x) (if (zero? x) 1 (* x (app f (sub1 x))))))) (app f 5)): passed
(letrec ((e (lambda (x) (if (zero? x) #t (app o (sub1 x))))) (o (lambda (x) (if (zero? x) #f (app e (sub1 x)))))) (app e 25)): passed
That’s all for this post, folks! This is one of the more involved parts in our tutorial. Yet we didn’t involve all the features that makes scheme procedures interesting: proper tail calls, closures. Although our implementation supports recursion, letrec is allowed only at the top of our program. Nevertheless, we did end up adding lambdas into our language!
Working code at the end of this step can be found at my Github repo with tag step_8_procedures.